D. Kennedy
Physics-informed Gaussian Process for Online Optimization of Particle Accelerators
Sep 08, 2020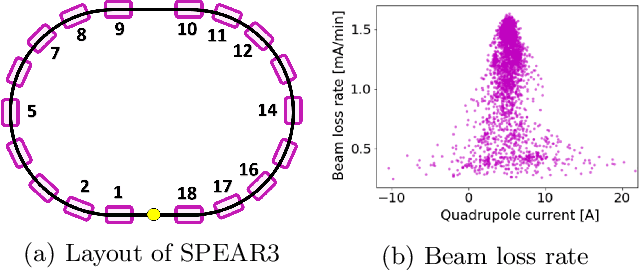
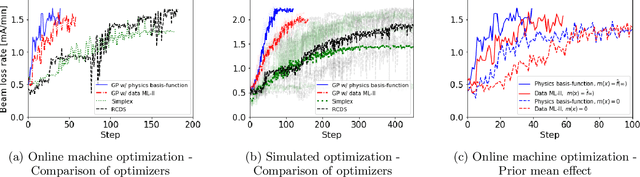
Abstract:High-dimensional optimization is a critical challenge for operating large-scale scientific facilities. We apply a physics-informed Gaussian process (GP) optimizer to tune a complex system by conducting efficient global search. Typical GP models learn from past observations to make predictions, but this reduces their applicability to new systems where archive data is not available. Instead, here we use a fast approximate model from physics simulations to design the GP model. The GP is then employed to make inferences from sequential online observations in order to optimize the system. Simulation and experimental studies were carried out to demonstrate the method for online control of a storage ring. We show that the physics-informed GP outperforms current routinely used online optimizers in terms of convergence speed, and robustness on this task. The ability to inform the machine-learning model with physics may have wide applications in science.
Online tuning and light source control using a physics-informed Gaussian process Adi
Nov 04, 2019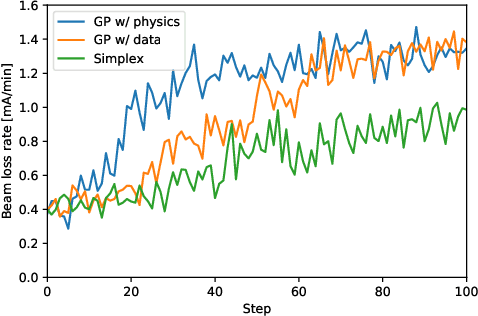
Abstract:Operating large-scale scientific facilities often requires fast tuning and robust control in a high dimensional space. In this paper we introduce a new physics-informed optimization algorithm based on Gaussian process regression. Our method takes advantage of the existing domain knowledge in the form of realizations of a physics model of the observed system. We have applied a physics-informed Gaussian Process method experimentally at the SPEAR3 storage ring to demonstrate online accelerator optimization. This method outperforms Gaussian Process trained on data as well as the standard approach routinely used for operation, in terms of convergence speed and optimal point. The proposed method could be applicable to automatic tuning and control of other complex systems, without a prerequisite for any observed data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge