Exact Matrix Seriation through Mathematical Optimization: Stress and Effectiveness-Based Models

Matrix seriation, the problem of permuting the rows and columns of a matrix to uncover latent structure, is a fundamental technique in data science, particularly in the visualization and analysis of relational data. Applications span clustering, anomaly detection, and beyond. In this work, we present a unified framework grounded in mathematical optimization to address matrix seriation from a rigorous, model-based perspective. Our approach leverages combinatorial and mixed-integer optimization to represent seriation objectives and constraints with high fidelity, bridging the gap between traditional heuristic methods and exact solution techniques. We introduce new mathematical programming models for neighborhood-based stress criteria, including nonlinear formulations and their linearized counterparts. For structured settings such as Moore and von Neumann neighborhoods, we develop a novel Hamiltonian path-based reformulation that enables effective control over spatial arrangement and interpretability in the reordered matrix. To assess the practical impact of our models, we carry out an extensive set of experiments on synthetic and real-world datasets, as well as on a newly curated benchmark based on a coauthorship network from the matrix seriation literature. Our results show that these optimization-based formulations not only enhance solution quality and interpretability but also provide a versatile foundation for extending matrix seriation to new domains in data science.

A Mathematical Programming Approach to Optimal Classification Forests

In this paper we propose a novel mathematical optimization based methodology to construct classification forests. A given number of trees are simultaneously constructed, each of them providing a predicted class for each of the observations in the training dataset. An observation is then classified to its most frequently predicted class. We give a mixed integer linear programming formulation for the problem. We report the results of our computational experiments. Our proposed method outperforms state-of-the-art tree-based classification methods on several standard datasets.

Multiclass Optimal Classification Trees with SVM-splits

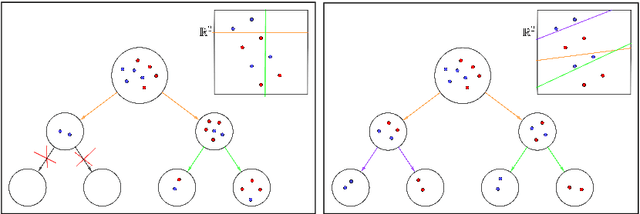
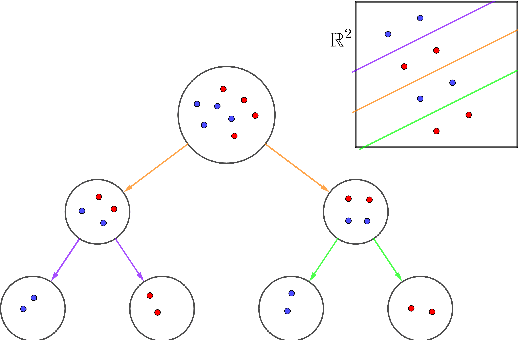
In this paper we present a novel mathematical optimization-based methodology to construct tree-shaped classification rules for multiclass instances. Our approach consists of building Classification Trees in which, except for the leaf nodes, the labels are temporarily left out and grouped into two classes by means of a SVM separating hyperplane. We provide a Mixed Integer Non Linear Programming formulation for the problem and report the results of an extended battery of computational experiments to assess the performance of our proposal with respect to other benchmarking classification methods.

Robust Optimal Classification Trees under Noisy Labels

In this paper we propose a novel methodology to construct Optimal Classification Trees that takes into account that noisy labels may occur in the training sample. Our approach rests on two main elements: (1) the splitting rules for the classification trees are designed to maximize the separation margin between classes applying the paradigm of SVM; and (2) some of the labels of the training sample are allowed to be changed during the construction of the tree trying to detect the label noise. Both features are considered and integrated together to design the resulting Optimal Classification Tree. We present a Mixed Integer Non Linear Programming formulation for the problem, suitable to be solved using any of the available off-the-shelf solvers. The model is analyzed and tested on a battery of standard datasets taken from UCI Machine Learning repository, showing the effectiveness of our approach.

A Mathematical Programming approach to Binary Supervised Classification with Label Noise

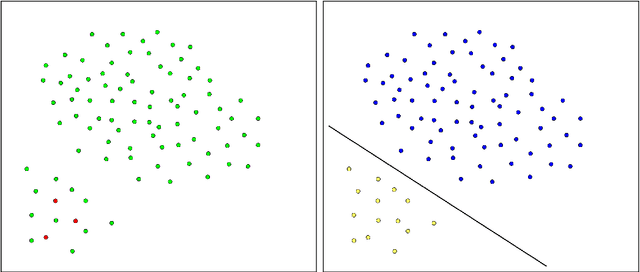
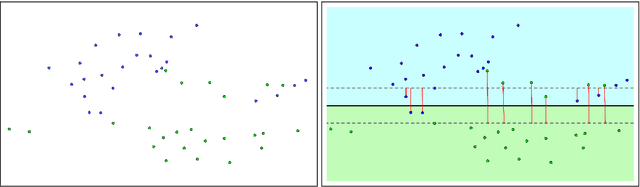
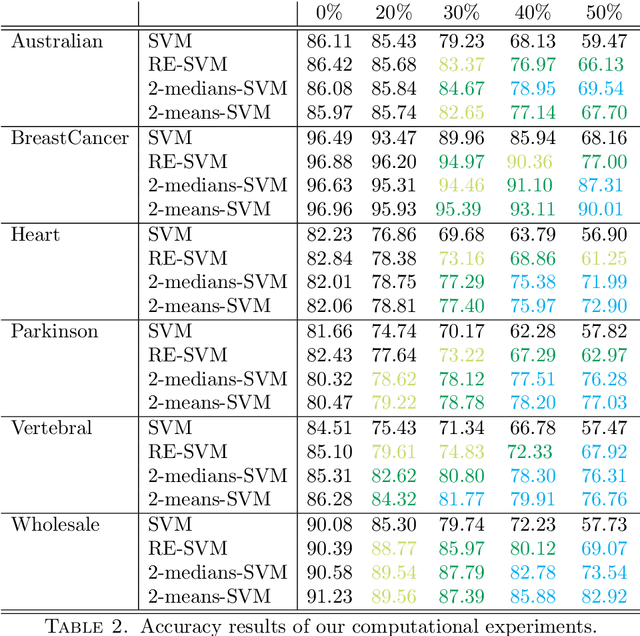
In this paper we propose novel methodologies to construct Support Vector Machine -based classifiers that takes into account that label noises occur in the training sample. We propose different alternatives based on solving Mixed Integer Linear and Non Linear models by incorporating decisions on relabeling some of the observations in the training dataset. The first method incorporates relabeling directly in the SVM model while a second family of methods combines clustering with classification at the same time, giving rise to a model that applies simultaneously similarity measures and SVM. Extensive computational experiments are reported based on a battery of standard datasets taken from UCI Machine Learning repository, showing the effectiveness of the proposed approaches.

Optimal arrangements of hyperplanes for multiclass classification

In this paper, we present a novel approach to construct multiclass clasifiers by means of arrangements of hyperplanes. We propose different mixed integer non linear programming formulations for the problem by using extensions of widely used measures for misclassifying observations. We prove that kernel tools can be extended to these models. Some strategies are detailed that help solving the associated mathematical programming problems more efficiently. An extensive battery of experiments has been run which reveal the powerfulness of our proposal in contrast to other previously proposed methods.