Unbiasing Enhanced Sampling on a High-dimensional Free Energy Surface with Deep Generative Model

Biased enhanced sampling methods utilizing collective variables (CVs) are powerful tools for sampling conformational ensembles. Due to high intrinsic dimensions, efficiently generating conformational ensembles for complex systems requires enhanced sampling on high-dimensional free energy surfaces. While methods like temperature-accelerated molecular dynamics (TAMD) can adopt many CVs in a simulation, unbiasing the simulation requires accurate modeling of a high-dimensional CV probability distribution, which is challenging for traditional density estimation techniques. Here we propose an unbiasing method based on the score-based diffusion model, a deep generative learning method that excels in density estimation across complex data landscapes. We test the score-based diffusion unbiasing method on TAMD simulations. The results demonstrate that this unbiasing approach significantly outperforms traditional unbiasing methods, and can generate accurate unbiased conformational ensembles for simulations with a number of CVs higher than usual ranges.

Reweighted Manifold Learning of Collective Variables from Enhanced Sampling Simulations

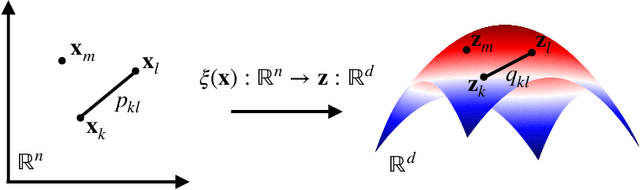
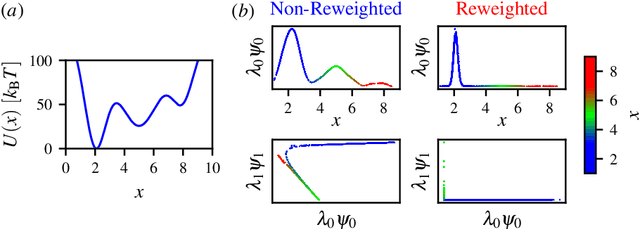
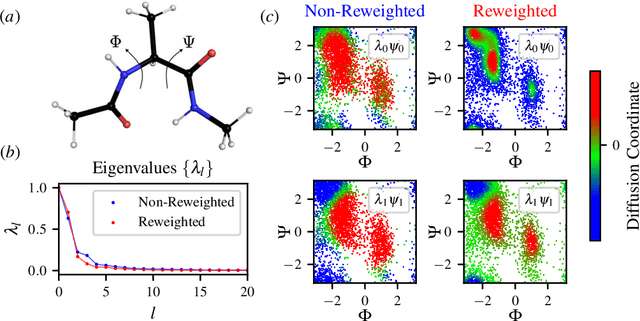
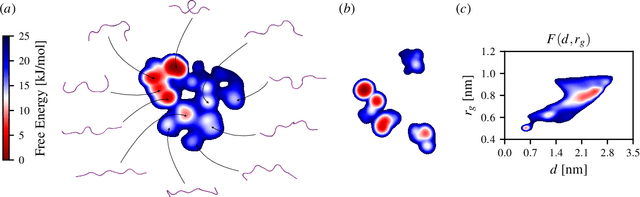
Enhanced sampling methods are indispensable in computational physics and chemistry, where atomistic simulations cannot exhaustively sample the high-dimensional configuration space of dynamical systems due to the sampling problem. A class of such enhanced sampling methods works by identifying a few slow degrees of freedom, termed collective variables (CVs), and enhancing the sampling along these CVs. Selecting CVs to analyze and drive the sampling is not trivial and often relies on physical and chemical intuition. Despite routinely circumventing this issue using manifold learning to estimate CVs directly from standard simulations, such methods cannot provide mappings to a low-dimensional manifold from enhanced sampling simulations as the geometry and density of the learned manifold are biased. Here, we address this crucial issue and provide a general reweighting framework based on anisotropic diffusion maps for manifold learning that takes into account that the learning data set is sampled from a biased probability distribution. We consider manifold learning methods based on constructing a Markov chain describing transition probabilities between high-dimensional samples. We show that our framework reverts the biasing effect yielding CVs that correctly describe the equilibrium density. This advancement enables the construction of low-dimensional CVs using manifold learning directly from data generated by enhanced sampling simulations. We call our framework reweighted manifold learning. We show that it can be used in many manifold learning techniques on data from both standard and enhanced sampling simulations.