Machine Learning of Slow Collective Variables and Enhanced Sampling via Spatial Techniques

Understanding the long-time dynamics of complex physical processes depends on our ability to recognize patterns. To simplify the description of these processes, we often introduce a set of reaction coordinates, customarily referred to as collective variables (CVs). The quality of these CVs heavily impacts our comprehension of the dynamics, often influencing the estimates of thermodynamics and kinetics from atomistic simulations. Consequently, identifying CVs poses a fundamental challenge in chemical physics. Recently, significant progress was made by leveraging the predictive ability of unsupervised machine learning techniques to determine CVs. Many of these techniques require temporal information to learn slow CVs that correspond to the long timescale behavior of the studied process. Here, however, we specifically focus on techniques that can identify CVs corresponding to the slowest transitions between states without needing temporal trajectories as input, instead using the spatial characteristics of the data. We discuss the latest developments in this category of techniques and briefly discuss potential directions for thermodynamics-informed spatial learning of slow CVs.

A Note on Spectral Map

In molecular dynamics (MD) simulations, transitions between states are often rare events due to energy barriers that exceed the thermal temperature. Because of their infrequent occurrence and the huge number of degrees of freedom in molecular systems, understanding the physical properties that drive rare events is immensely difficult. A common approach to this problem is to propose a collective variable (CV) that describes this process by a simplified representation. However, choosing CVs is not easy, as it often relies on physical intuition. Machine learning (ML) techniques provide a promising approach for effectively extracting optimal CVs from MD data. Here, we provide a note on a recent unsupervised ML method called spectral map, which constructs CVs by maximizing the timescale separation between slow and fast variables in the system.

Spectral Map for Slow Collective Variables, Markovian Dynamics, and Transition State Ensembles

Understanding the behavior of complex molecular systems is a fundamental problem in physical chemistry. To describe the long-time dynamics of such systems, which is responsible for their most informative characteristics, we can identify a few slow collective variables (CVs) while treating the remaining fast variables as thermal noise. This enables us to simplify the dynamics and treat it as diffusion in a free-energy landscape spanned by slow CVs, effectively rendering the dynamics Markovian. Our recent statistical learning technique, spectral map [Rydzewski, J. Phys. Chem. Lett. 2023, 14, 22, 5216-5220], explores this strategy to learn slow CVs by maximizing a spectral gap of a transition matrix. In this work, we introduce several advancements into our framework, using a high-dimensional reversible folding process of a protein as an example. We implement an algorithm for coarse-graining Markov transition matrices to partition the reduced space of slow CVs kinetically and use it to define a transition state ensemble. We show that slow CVs learned by spectral map closely approach the Markovian limit for an overdamped diffusion. We demonstrate that coordinate-dependent diffusion coefficients only slightly affect the constructed free-energy landscapes. Finally, we present how spectral map can be used to quantify the importance of features and compare slow CVs with structural descriptors commonly used in protein folding. Overall, we demonstrate that a single slow CV learned by spectral map can be used as a physical reaction coordinate to capture essential characteristics of protein folding.

Reweighted Manifold Learning of Collective Variables from Enhanced Sampling Simulations

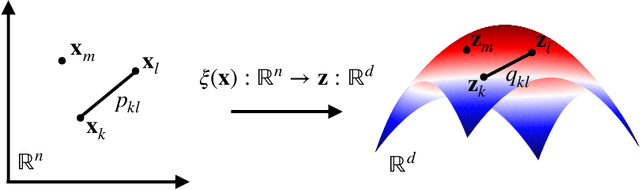
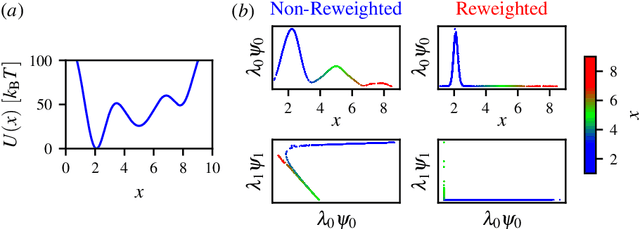
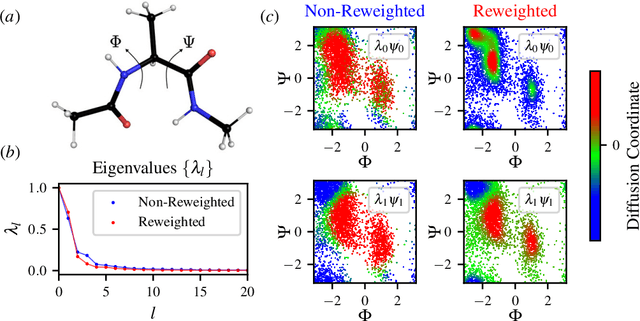
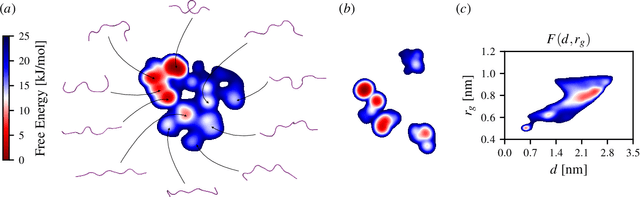
Enhanced sampling methods are indispensable in computational physics and chemistry, where atomistic simulations cannot exhaustively sample the high-dimensional configuration space of dynamical systems due to the sampling problem. A class of such enhanced sampling methods works by identifying a few slow degrees of freedom, termed collective variables (CVs), and enhancing the sampling along these CVs. Selecting CVs to analyze and drive the sampling is not trivial and often relies on physical and chemical intuition. Despite routinely circumventing this issue using manifold learning to estimate CVs directly from standard simulations, such methods cannot provide mappings to a low-dimensional manifold from enhanced sampling simulations as the geometry and density of the learned manifold are biased. Here, we address this crucial issue and provide a general reweighting framework based on anisotropic diffusion maps for manifold learning that takes into account that the learning data set is sampled from a biased probability distribution. We consider manifold learning methods based on constructing a Markov chain describing transition probabilities between high-dimensional samples. We show that our framework reverts the biasing effect yielding CVs that correctly describe the equilibrium density. This advancement enables the construction of low-dimensional CVs using manifold learning directly from data generated by enhanced sampling simulations. We call our framework reweighted manifold learning. We show that it can be used in many manifold learning techniques on data from both standard and enhanced sampling simulations.