From Displacements to Distributions: A Machine-Learning Enabled Framework for Quantifying Uncertainties in Parameters of Computational Models

This work presents novel extensions for combining two frameworks for quantifying both aleatoric (i.e., irreducible) and epistemic (i.e., reducible) sources of uncertainties in the modeling of engineered systems. The data-consistent (DC) framework poses an inverse problem and solution for quantifying aleatoric uncertainties in terms of pullback and push-forward measures for a given Quantity of Interest (QoI) map. Unfortunately, a pre-specified QoI map is not always available a priori to the collection of data associated with system outputs. The data themselves are often polluted with measurement errors (i.e., epistemic uncertainties), which complicates the process of specifying a useful QoI. The Learning Uncertain Quantities (LUQ) framework defines a formal three-step machine-learning enabled process for transforming noisy datasets into samples of a learned QoI map to enable DC-based inversion. We develop a robust filtering step in LUQ that can learn the most useful quantitative information present in spatio-temporal datasets. The learned QoI map transforms simulated and observed datasets into distributions to perform DC-based inversion. We also develop a DC-based inversion scheme that iterates over time as new spatial datasets are obtained and utilizes quantitative diagnostics to identify both the quality and impact of inversion at each iteration. Reproducing Kernel Hilbert Space theory is leveraged to mathematically analyze the learned QoI map and develop a quantitative sufficiency test for evaluating the filtered data. An illustrative example is utilized throughout while the final two examples involve the manufacturing of shells of revolution to demonstrate various aspects of the presented frameworks.

Learning Quantities of Interest from Dynamical Systems for Observation-Consistent Inversion

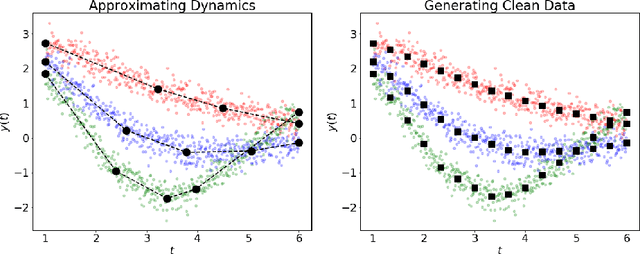
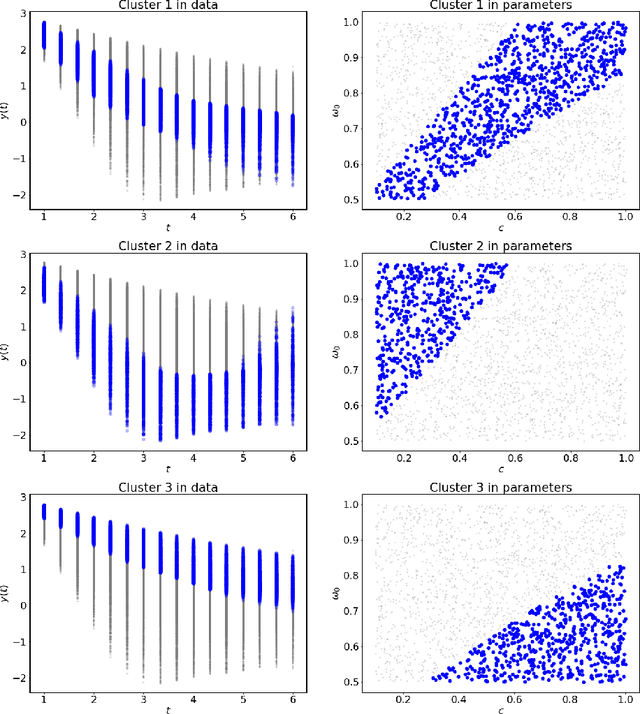
Dynamical systems arise in a wide variety of mathematical models from science and engineering. A common challenge is to quantify uncertainties on model inputs (parameters) that correspond to a quantitative characterization of uncertainties on observable Quantities of Interest (QoI). To this end, we consider a stochastic inverse problem (SIP) with a solution described by a pullback probability measure. We call this an observation-consistent solution, as its subsequent push-forward through the QoI map matches the observed probability distribution on model outputs. A distinction is made between QoI useful for solving the SIP and arbitrary model output data. In dynamical systems, model output data are often given as a series of state variable responses recorded over a particular time window. Consequently, the dimension of output data can easily exceed $\mathcal{O}(1E4)$ or more due to the frequency of observations, and the correct choice or construction of a QoI from this data is not self-evident. We present a new framework, Learning Uncertain Quantities (LUQ), that facilitates the tractable solution of SIPs for dynamical systems. Given ensembles of predicted (simulated) time series and (noisy) observed data, LUQ provides routines for filtering data, unsupervised learning of the underlying dynamics, classifying observations, and feature extraction to learn the QoI map. Subsequently, time series data are transformed into samples of the underlying predicted and observed distributions associated with the QoI so that solutions to the SIP are computable. Following the introduction and demonstration of LUQ, numerical results from several SIPs are presented for a variety of dynamical systems arising in the life and physical sciences. For scientific reproducibility, we provide links to our Python implementation of LUQ and to all data and scripts required to reproduce the results in this manuscript.