Data Representation and Compression Using Linear-Programming Approximations

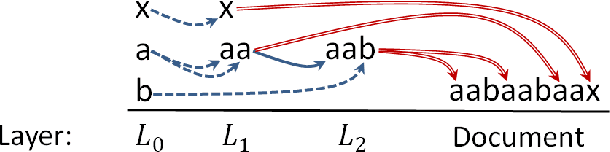
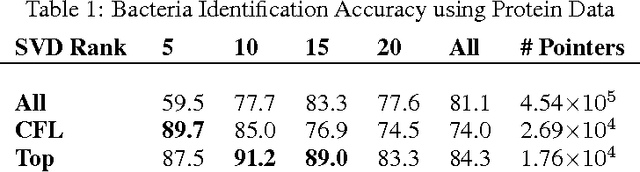
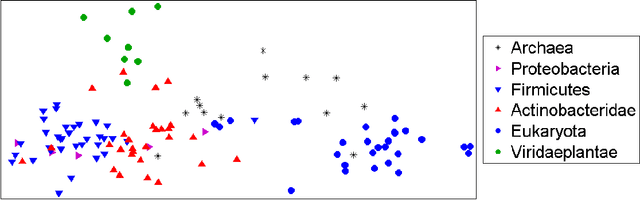
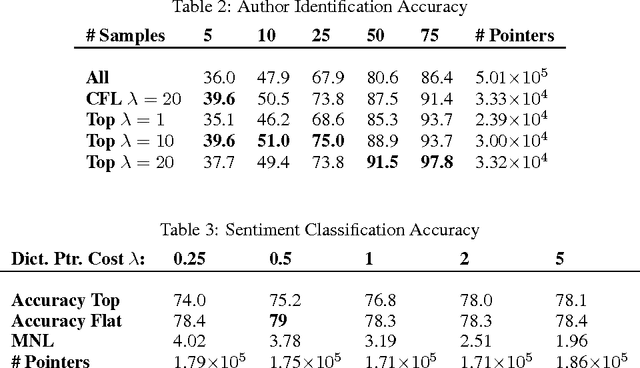
We propose `Dracula', a new framework for unsupervised feature selection from sequential data such as text. Dracula learns a dictionary of $n$-grams that efficiently compresses a given corpus and recursively compresses its own dictionary; in effect, Dracula is a `deep' extension of Compressive Feature Learning. It requires solving a binary linear program that may be relaxed to a linear program. Both problems exhibit considerable structure, their solution paths are well behaved, and we identify parameters which control the depth and diversity of the dictionary. We also discuss how to derive features from the compressed documents and show that while certain unregularized linear models are invariant to the structure of the compressed dictionary, this structure may be used to regularize learning. Experiments are presented that demonstrate the efficacy of Dracula's features.

Learning Mixed Graphical Models

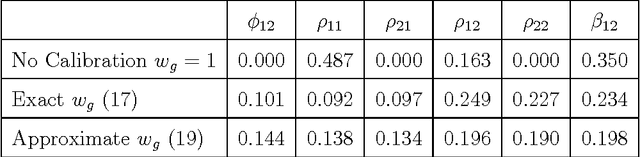
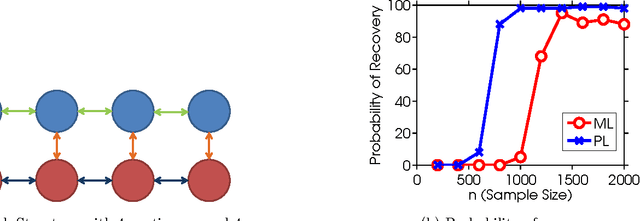
We consider the problem of learning the structure of a pairwise graphical model over continuous and discrete variables. We present a new pairwise model for graphical models with both continuous and discrete variables that is amenable to structure learning. In previous work, authors have considered structure learning of Gaussian graphical models and structure learning of discrete models. Our approach is a natural generalization of these two lines of work to the mixed case. The penalization scheme involves a novel symmetric use of the group-lasso norm and follows naturally from a particular parametrization of the model.

Nonlinear Estimators and Tail Bounds for Dimension Reduction in $l_1$ Using Cauchy Random Projections

For dimension reduction in $l_1$, the method of {\em Cauchy random projections} multiplies the original data matrix $\mathbf{A} \in\mathbb{R}^{n\times D}$ with a random matrix $\mathbf{R} \in \mathbb{R}^{D\times k}$ ($k\ll\min(n,D)$) whose entries are i.i.d. samples of the standard Cauchy C(0,1). Because of the impossibility results, one can not hope to recover the pairwise $l_1$ distances in $\mathbf{A}$ from $\mathbf{B} = \mathbf{AR} \in \mathbb{R}^{n\times k}$, using linear estimators without incurring large errors. However, nonlinear estimators are still useful for certain applications in data stream computation, information retrieval, learning, and data mining. We propose three types of nonlinear estimators: the bias-corrected sample median estimator, the bias-corrected geometric mean estimator, and the bias-corrected maximum likelihood estimator. The sample median estimator and the geometric mean estimator are asymptotically (as $k\to \infty$) equivalent but the latter is more accurate at small $k$. We derive explicit tail bounds for the geometric mean estimator and establish an analog of the Johnson-Lindenstrauss (JL) lemma for dimension reduction in $l_1$, which is weaker than the classical JL lemma for dimension reduction in $l_2$. Asymptotically, both the sample median estimator and the geometric mean estimators are about 80% efficient compared to the maximum likelihood estimator (MLE). We analyze the moments of the MLE and propose approximating the distribution of the MLE by an inverse Gaussian.