Autonomous Bootstrapping of Quantum Dot Devices

Semiconductor quantum dots (QD) are a promising platform for multiple different qubit implementations, all of which are voltage-controlled by programmable gate electrodes. However, as the QD arrays grow in size and complexity, tuning procedures that can fully autonomously handle the increasing number of control parameters are becoming essential for enabling scalability. We propose a bootstrapping algorithm for initializing a depletion mode QD device in preparation for subsequent phases of tuning. During bootstrapping, the QD device functionality is validated, all gates are characterized, and the QD charge sensor is made operational. We demonstrate the bootstrapping protocol in conjunction with a coarse tuning module, showing that the combined algorithm can efficiently and reliably take a cooled-down QD device to a desired global state configuration in under 8 minutes with a success rate of 96 %. Importantly, by following heuristic approaches to QD device initialization and combining the efficient ray-based measurement with the rapid radio-frequency reflectometry measurements, the proposed algorithm establishes a reference in terms of performance, reliability, and efficiency against which alternative algorithms can be benchmarked.

Estimation of Convex Polytopes for Automatic Discovery of Charge State Transitions in Quantum Dot Arrays

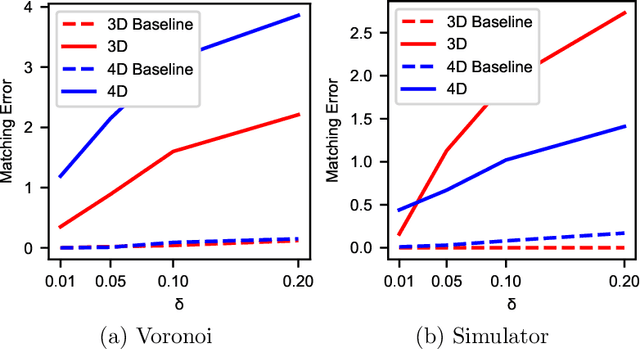
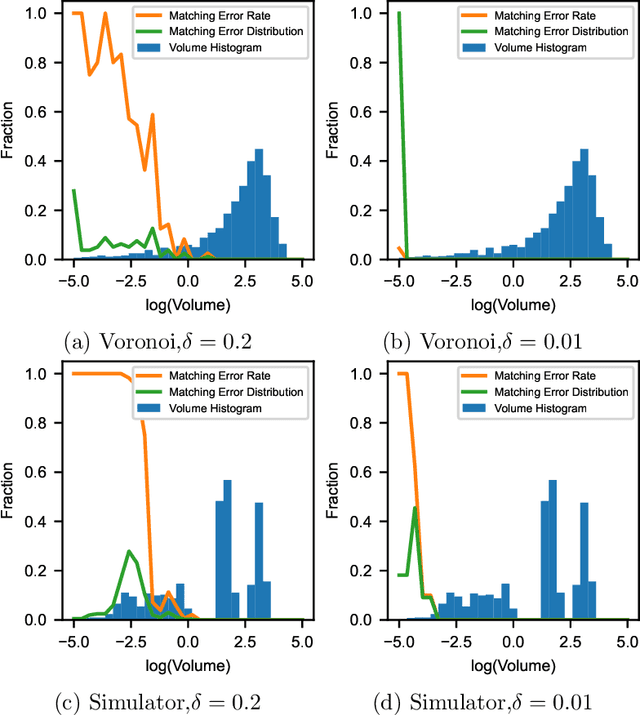
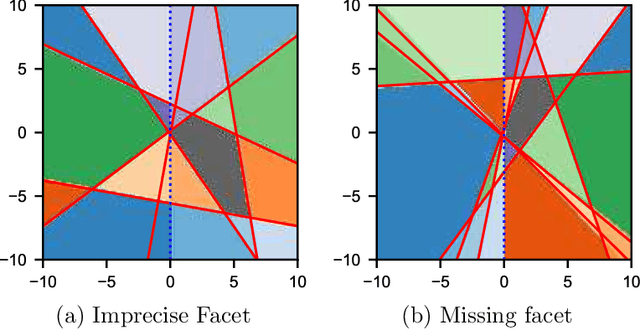
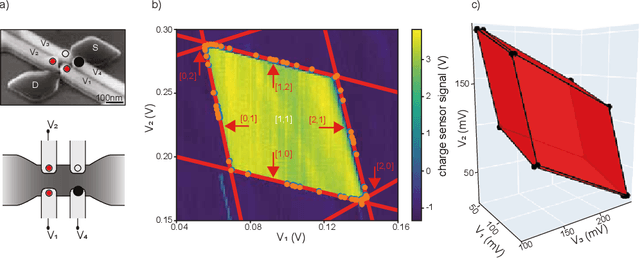
In spin based quantum dot arrays, a leading technology for quantum computation applications, material or fabrication imprecisions affect the behaviour of the device, which is compensated via tuning parameters. Automatic tuning of these device parameters constitutes a formidable challenge for machine-learning. Here, we present the first practical algorithm for controlling the transition of electrons in a spin qubit array. We exploit a connection to computational geometry and phrase the task as estimating a convex polytope from measurements. Our proposed algorithm uses active learning, to find the count, shapes and sizes of all facets of a given polytope. We test our algorithm on artifical polytopes as well as a real 2x2 spin qubit array. Our results show that we can reliably find the facets of the polytope, including small facets with sizes on the order of the measurement precision. We discuss the implications of the NP-hardness of the underlying estimation problem and outline design considerations, limitations and tuning strategies for controlling future large-scale spin qubit devices.