YOLO-based Object Detection in Industry 4.0 Fischertechnik Model Environment

In this paper we extensively explore the suitability of YOLO architectures to monitor the process flow across a Fischertechnik industry 4.0 application. Specifically, different YOLO architectures in terms of size and complexity design along with different prior-shapes assignment strategies are adopted. To simulate the real world factory environment, we prepared a rich dataset augmented with different distortions that highly enhance and in some cases degrade our image qualities. The degradation is performed to account for environmental variations and enhancements opt to compensate the color correlations that we face while preparing our dataset. The analysis of our conducted experiments shows the effectiveness of the presented approach evaluated using different measures along with the training and validation strategies that we tailored to tackle the unavoidable color correlations that the problem at hand inherits by nature.

Adaptive Neural Domain Refinement for Solving Time-Dependent Differential Equations

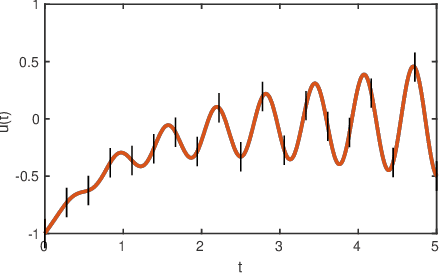
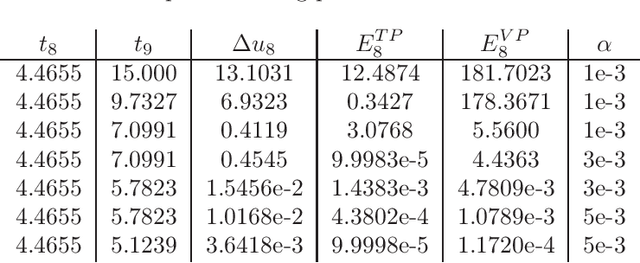
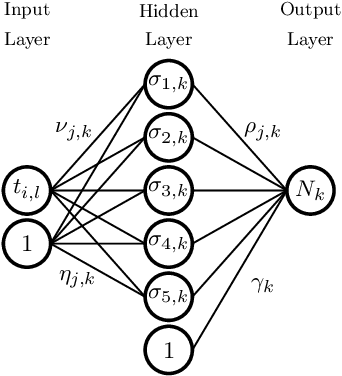
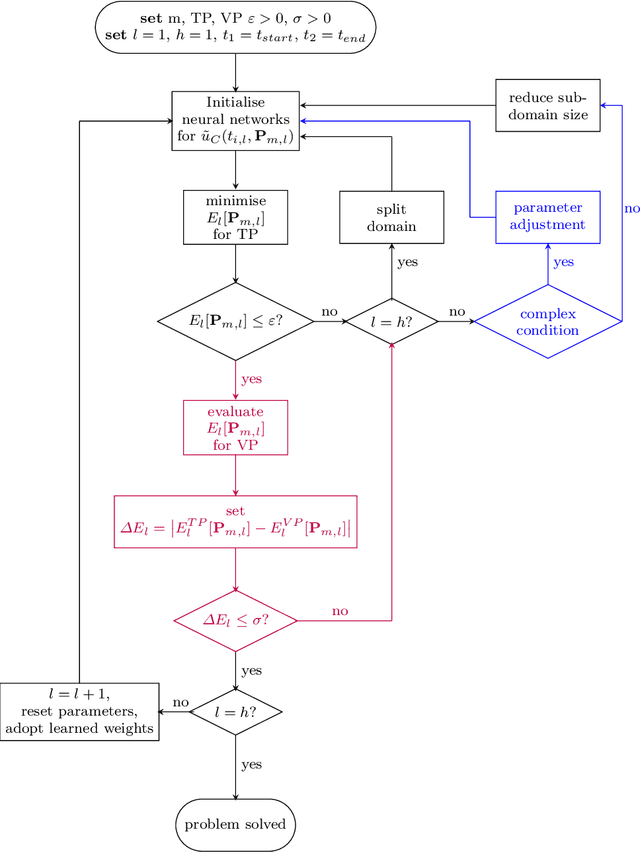
A classic approach for solving differential equations with neural networks builds upon neural forms, in which a cost function can be constructed directly using the differential equation with a discretisation of the solution domain. Making use of neural forms for time-dependent differential equations, one can apply the recently developed method of domain fragmentation. That is, the domain may be split into several subdomains, on which the optimisation problem is solved. In classic adaptive numerical methods for solving differential equations, the mesh as well as the domain may be refined or decomposed, respectively, in order to improve accuracy. Also the degree of approximation accuracy may be adapted. It would be desirable to transfer such important and successful strategies to the field of neural network based solutions. In the present work, we propose a novel adaptive neural approach to meet this aim for solving time-dependent problems. To this end, each subdomain is reduced in size until the optimisation is resolved up to a predefined training accuracy. In addition, while the neural networks employed are by default small, the number of neurons may also be adjusted in an adaptive way. We introduce conditions to automatically confirm the solution reliability and optimise computational parameters whenever it is necessary. We provide results for three carefully chosen example initial value problems and illustrate important properties of the method alongside.

Collocation Polynomial Neural Forms and Domain Fragmentation for Initial Value Problems

Several neural network approaches for solving differential equations employ trial solutions with a feedforward neural network. There are different means to incorporate the trial solution in the construction, for instance one may include them directly in the cost function. Used within the corresponding neural network, the trial solutions define the so-called neural form. Such neural forms represent general, flexible tools by which one may solve various differential equations. In this article we consider time-dependent initial value problems, which require to set up the neural form framework adequately. The neural forms presented up to now in the literature for such a setting can be considered as first order polynomials. In this work we propose to extend the polynomial order of the neural forms. The novel collocation-type construction includes several feedforward neural networks, one for each order. Additionally, we propose the fragmentation of the computational domain into subdomains. The neural forms are solved on each subdomain, whereas the interfacing grid points overlap in order to provide initial values over the whole fragmentation. We illustrate in experiments that the combination of collocation neural forms of higher order and the domain fragmentation allows to solve initial value problems over large domains with high accuracy and reliability.

Computational characteristics of feedforward neural networks for solving a stiff differential equation

Feedforward neural networks offer a promising approach for solving differential equations. However, the reliability and accuracy of the approximation still represent delicate issues that are not fully resolved in the current literature. Computational approaches are in general highly dependent on a variety of computational parameters as well as on the choice of optimisation methods, a point that has to be seen together with the structure of the cost function. The intention of this paper is to make a step towards resolving these open issues. To this end we study here the solution of a simple but fundamental stiff ordinary differential equation modelling a damped system. We consider two computational approaches for solving differential equations by neural forms. These are the classic but still actual method of trial solutions defining the cost function, and a recent direct construction of the cost function related to the trial solution method. Let us note that the settings we study can easily be applied more generally, including solution of partial differential equations. By a very detailed computational study we show that it is possible to identify preferable choices to be made for parameters and methods. We also illuminate some interesting effects that are observable in the neural network simulations. Overall we extend the current literature in the field by showing what can be done in order to obtain reliable and accurate results by the neural network approach. By doing this we illustrate the importance of a careful choice of the computational setup.