Adaptive Neural Domain Refinement for Solving Time-Dependent Differential Equations
Paper and Code
Dec 23, 2021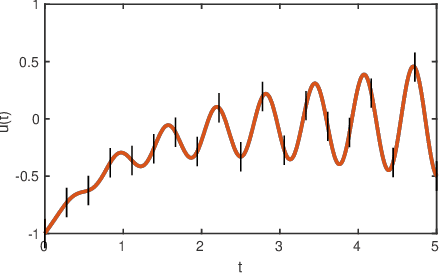
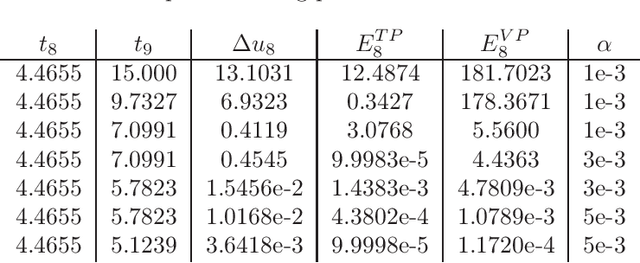
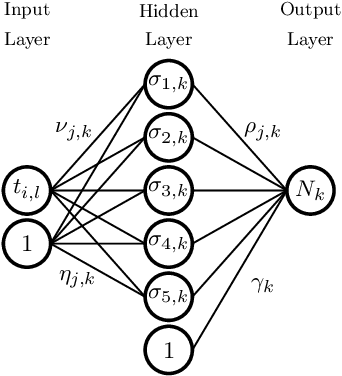
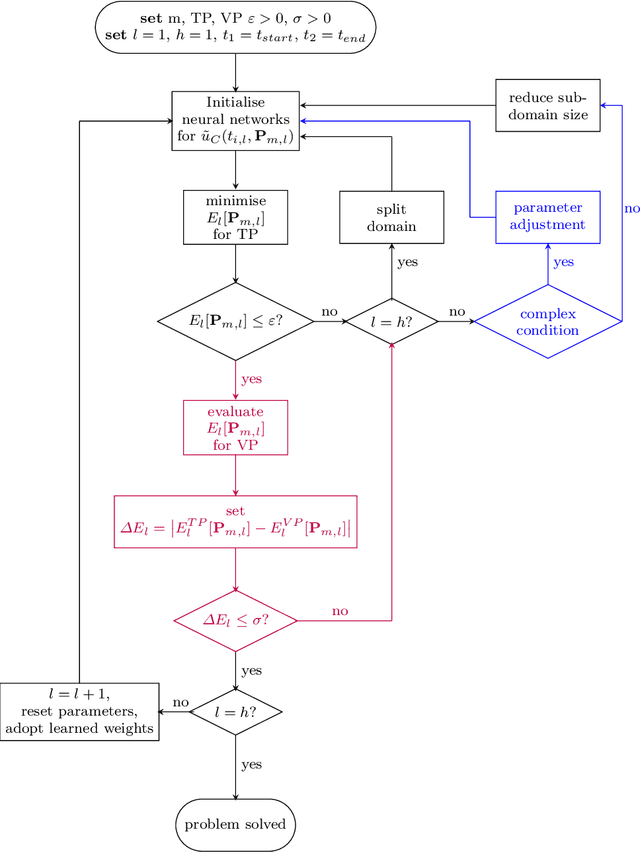
A classic approach for solving differential equations with neural networks builds upon neural forms, in which a cost function can be constructed directly using the differential equation with a discretisation of the solution domain. Making use of neural forms for time-dependent differential equations, one can apply the recently developed method of domain fragmentation. That is, the domain may be split into several subdomains, on which the optimisation problem is solved. In classic adaptive numerical methods for solving differential equations, the mesh as well as the domain may be refined or decomposed, respectively, in order to improve accuracy. Also the degree of approximation accuracy may be adapted. It would be desirable to transfer such important and successful strategies to the field of neural network based solutions. In the present work, we propose a novel adaptive neural approach to meet this aim for solving time-dependent problems. To this end, each subdomain is reduced in size until the optimisation is resolved up to a predefined training accuracy. In addition, while the neural networks employed are by default small, the number of neurons may also be adjusted in an adaptive way. We introduce conditions to automatically confirm the solution reliability and optimise computational parameters whenever it is necessary. We provide results for three carefully chosen example initial value problems and illustrate important properties of the method alongside.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge