Tongyi Liang
Linear Dynamics-embedded Neural Network for Long-Sequence Modeling
Feb 23, 2024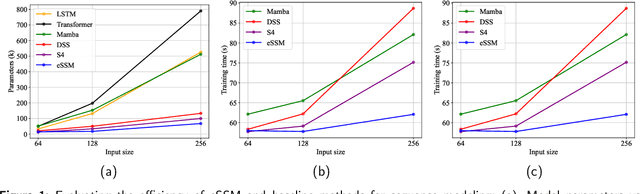

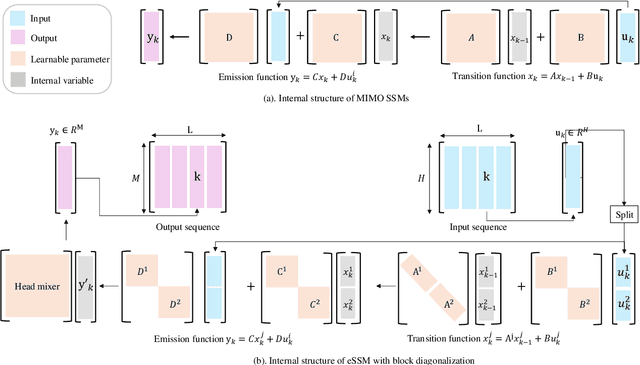
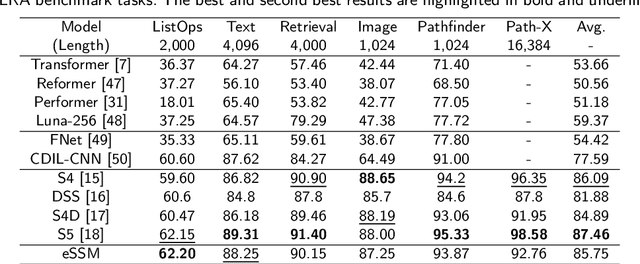
Abstract:The trade-off between performance and computational efficiency in long-sequence modeling becomes a bottleneck for existing models. Inspired by the continuous state space models (SSMs) with multi-input and multi-output in control theory, we propose a new neural network called Linear Dynamics-embedded Neural Network (LDNN). SSMs' continuous, discrete, and convolutional properties enable LDNN to have few parameters, flexible inference, and efficient training in long-sequence tasks. Two efficient strategies, diagonalization and $'\text{Disentanglement then Fast Fourier Transform (FFT)}'$, are developed to reduce the time complexity of convolution from $O(LNH\max\{L, N\})$ to $O(LN\max \{H, \log L\})$. We further improve LDNN through bidirectional noncausal and multi-head settings to accommodate a broader range of applications. Extensive experiments on the Long Range Arena (LRA) demonstrate the effectiveness and state-of-the-art performance of LDNN.
Spatiotemporal Observer Design for Predictive Learning of High-Dimensional Data
Feb 23, 2024



Abstract:Although deep learning-based methods have shown great success in spatiotemporal predictive learning, the framework of those models is designed mainly by intuition. How to make spatiotemporal forecasting with theoretical guarantees is still a challenging issue. In this work, we tackle this problem by applying domain knowledge from the dynamical system to the framework design of deep learning models. An observer theory-guided deep learning architecture, called Spatiotemporal Observer, is designed for predictive learning of high dimensional data. The characteristics of the proposed framework are twofold: firstly, it provides the generalization error bound and convergence guarantee for spatiotemporal prediction; secondly, dynamical regularization is introduced to enable the model to learn system dynamics better during training. Further experimental results show that this framework could capture the spatiotemporal dynamics and make accurate predictions in both one-step-ahead and multi-step-ahead forecasting scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge