Linear Dynamics-embedded Neural Network for Long-Sequence Modeling
Paper and Code
Feb 23, 2024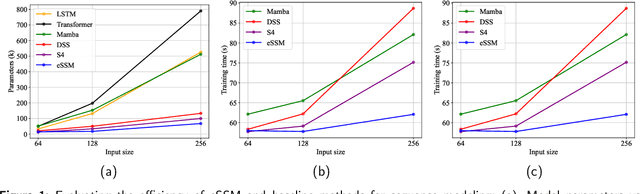

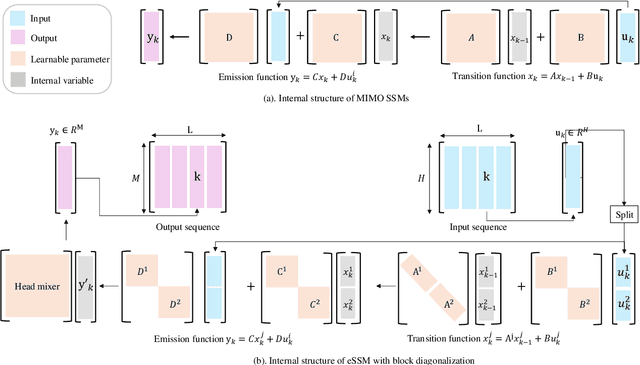
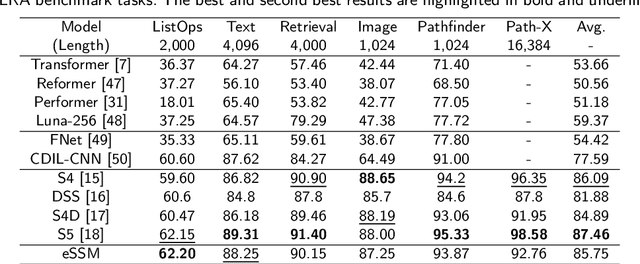
The trade-off between performance and computational efficiency in long-sequence modeling becomes a bottleneck for existing models. Inspired by the continuous state space models (SSMs) with multi-input and multi-output in control theory, we propose a new neural network called Linear Dynamics-embedded Neural Network (LDNN). SSMs' continuous, discrete, and convolutional properties enable LDNN to have few parameters, flexible inference, and efficient training in long-sequence tasks. Two efficient strategies, diagonalization and $'\text{Disentanglement then Fast Fourier Transform (FFT)}'$, are developed to reduce the time complexity of convolution from $O(LNH\max\{L, N\})$ to $O(LN\max \{H, \log L\})$. We further improve LDNN through bidirectional noncausal and multi-head settings to accommodate a broader range of applications. Extensive experiments on the Long Range Arena (LRA) demonstrate the effectiveness and state-of-the-art performance of LDNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge