Tomas Ortega
Communication Compression for Distributed Learning without Control Variates
Dec 05, 2024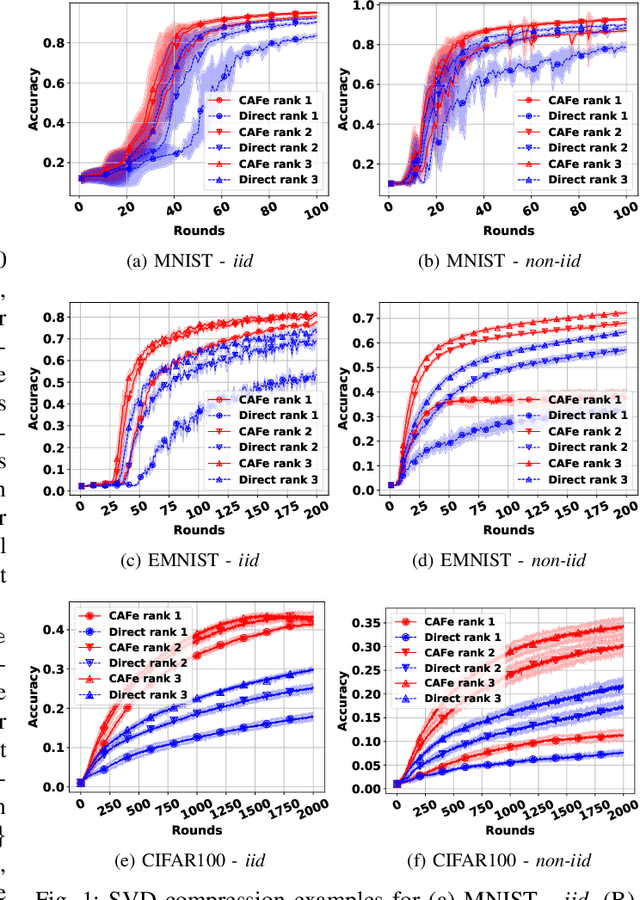
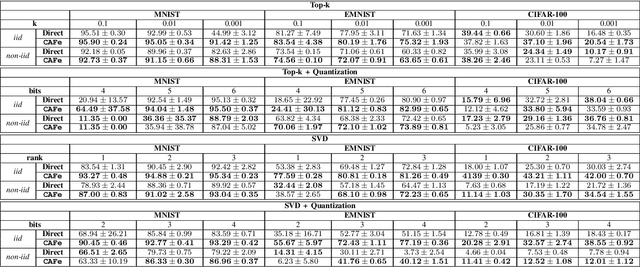
Abstract:Distributed learning algorithms, such as the ones employed in Federated Learning (FL), require communication compression to reduce the cost of client uploads. The compression methods used in practice are often biased, which require error feedback to achieve convergence when the compression is aggressive. In turn, error feedback requires client-specific control variates, which directly contradicts privacy-preserving principles and requires stateful clients. In this paper, we propose Compressed Aggregate Feedback (CAFe), a novel distributed learning framework that allows highly compressible client updates by exploiting past aggregated updates, and does not require control variates. We consider Distributed Gradient Descent (DGD) as a representative algorithm and provide a theoretical proof of CAFe's superiority to Distributed Compressed Gradient Descent (DCGD) with biased compression in the non-smooth regime with bounded gradient dissimilarity. Experimental results confirm that CAFe consistently outperforms distributed learning with direct compression and highlight the compressibility of the client updates with CAFe.
Decentralized Optimization in Time-Varying Networks with Arbitrary Delays
May 29, 2024Abstract:We consider a decentralized optimization problem for networks affected by communication delays. Examples of such networks include collaborative machine learning, sensor networks, and multi-agent systems. To mimic communication delays, we add virtual non-computing nodes to the network, resulting in directed graphs. This motivates investigating decentralized optimization solutions on directed graphs. Existing solutions assume nodes know their out-degrees, resulting in limited applicability. To overcome this limitation, we introduce a novel gossip-based algorithm, called DT-GO, that does not need to know the out-degrees. The algorithm is applicable in general directed networks, for example networks with delays or limited acknowledgment capabilities. We derive convergence rates for both convex and non-convex objectives, showing that our algorithm achieves the same complexity order as centralized Stochastic Gradient Descent. In other words, the effects of the graph topology and delays are confined to higher-order terms. Additionally, we extend our analysis to accommodate time-varying network topologies. Numerical simulations are provided to support our theoretical findings.
Decentralized Optimization in Networks with Arbitrary Delays
Jan 20, 2024Abstract:We consider the problem of decentralized optimization in networks with communication delays. To accommodate delays, we need decentralized optimization algorithms that work on directed graphs. Existing approaches require nodes to know their out-degree to achieve convergence. We propose a novel gossip-based algorithm that circumvents this requirement, allowing decentralized optimization in networks with communication delays. We prove that our algorithm converges on non-convex objectives, with the same main complexity order term as centralized Stochastic Gradient Descent (SGD), and show that the graph topology and the delays only affect the higher order terms. We provide numerical simulations that illustrate our theoretical results.
Asynchronous Federated Learning with Bidirectional Quantized Communications and Buffered Aggregation
Aug 01, 2023Abstract:Asynchronous Federated Learning with Buffered Aggregation (FedBuff) is a state-of-the-art algorithm known for its efficiency and high scalability. However, it has a high communication cost, which has not been examined with quantized communications. To tackle this problem, we present a new algorithm (QAFeL), with a quantization scheme that establishes a shared "hidden" state between the server and clients to avoid the error propagation caused by direct quantization. This approach allows for high precision while significantly reducing the data transmitted during client-server interactions. We provide theoretical convergence guarantees for QAFeL and corroborate our analysis with experiments on a standard benchmark.
Gossiped and Quantized Online Multi-Kernel Learning
Jan 24, 2023Abstract:In instances of online kernel learning where little prior information is available and centralized learning is unfeasible, past research has shown that distributed and online multi-kernel learning provides sub-linear regret as long as every pair of nodes in the network can communicate (i.e., the communications network is a complete graph). In addition, to manage the communication load, which is often a performance bottleneck, communications between nodes can be quantized. This letter expands on these results to non-fully connected graphs, which is often the case in wireless sensor networks. To address this challenge, we propose a gossip algorithm and provide a proof that it achieves sub-linear regret. Experiments with real datasets confirm our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge