Combined track finding with GNN & CKF

The application of Graph Neural Networks (GNN) in track reconstruction is a promising approach to cope with the challenges arising at the High-Luminosity upgrade of the Large Hadron Collider (HL-LHC). GNNs show good track-finding performance in high-multiplicity scenarios and are naturally parallelizable on heterogeneous compute architectures. Typical high-energy-physics detectors have high resolution in the innermost layers to support vertex reconstruction but lower resolution in the outer parts. GNNs mainly rely on 3D space-point information, which can cause reduced track-finding performance in the outer regions. In this contribution, we present a novel combination of GNN-based track finding with the classical Combinatorial Kalman Filter (CKF) algorithm to circumvent this issue: The GNN resolves the track candidates in the inner pixel region, where 3D space points can represent measurements very well. These candidates are then picked up by the CKF in the outer regions, where the CKF performs well even for 1D measurements. Using the ACTS infrastructure, we present a proof of concept based on truth tracking in the pixels as well as a dedicated GNN pipeline trained on $t\bar{t}$ events with pile-up 200 in the OpenDataDetector.

Gauge-equivariant pooling layers for preconditioners in lattice QCD

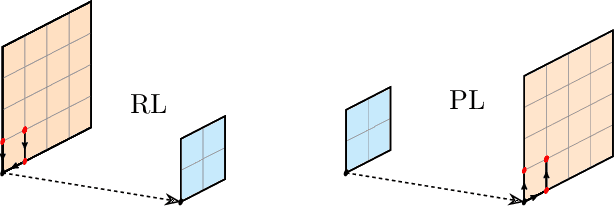
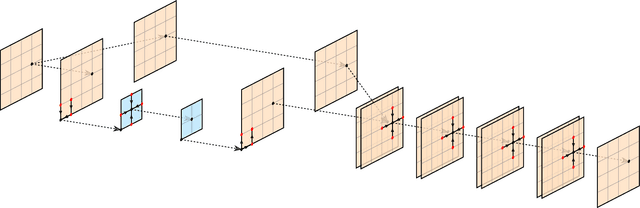
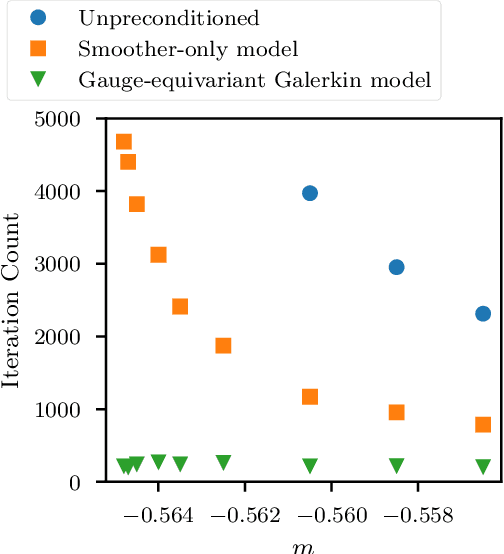
We demonstrate that gauge-equivariant pooling and unpooling layers can perform as well as traditional restriction and prolongation layers in multigrid preconditioner models for lattice QCD. These layers introduce a gauge degree of freedom on the coarse grid, allowing for the use of explicitly gauge-equivariant layers on the coarse grid. We investigate the construction of coarse-grid gauge fields and study their efficiency in the preconditioner model. We show that a combined multigrid neural network using a Galerkin construction for the coarse-grid gauge field eliminates critical slowing down.

Gauge-equivariant neural networks as preconditioners in lattice QCD

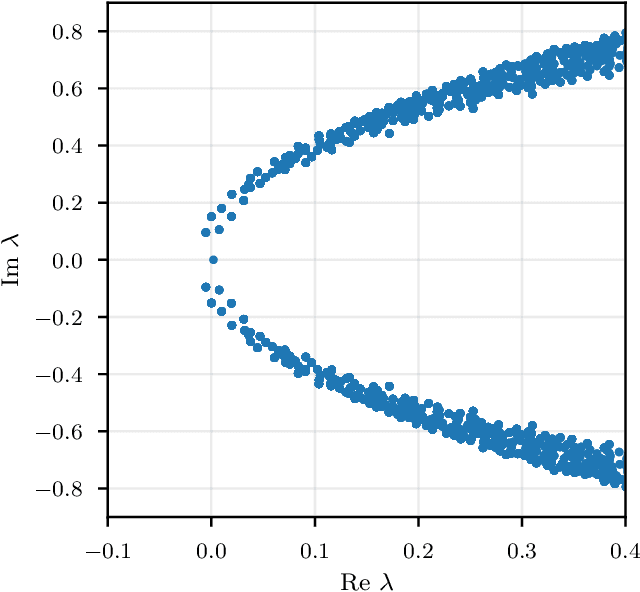
We demonstrate that a state-of-the art multi-grid preconditioner can be learned efficiently by gauge-equivariant neural networks. We show that the models require minimal re-training on different gauge configurations of the same gauge ensemble and to a large extent remain efficient under modest modifications of ensemble parameters. We also demonstrate that important paradigms such as communication avoidance are straightforward to implement in this framework.

Differentiated uniformization: A new method for inferring Markov chains on combinatorial state spaces including stochastic epidemic models

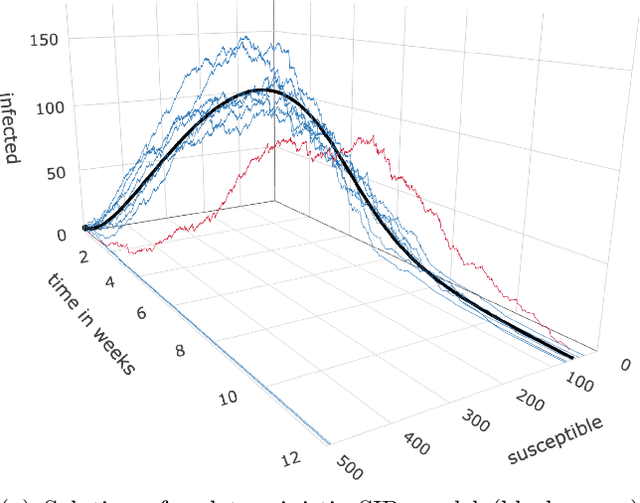
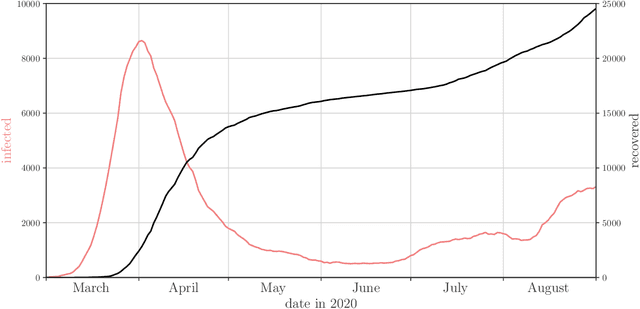
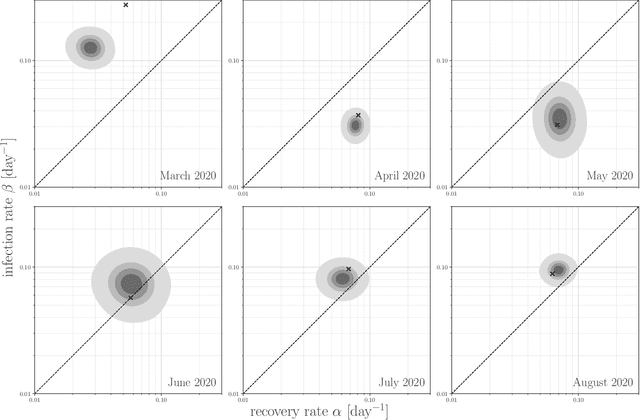
Motivation: We consider continuous-time Markov chains that describe the stochastic evolution of a dynamical system by a transition-rate matrix $Q$ which depends on a parameter $\theta$. Computing the probability distribution over states at time $t$ requires the matrix exponential $\exp(tQ)$, and inferring $\theta$ from data requires its derivative $\partial\exp\!(tQ)/\partial\theta$. Both are challenging to compute when the state space and hence the size of $Q$ is huge. This can happen when the state space consists of all combinations of the values of several interacting discrete variables. Often it is even impossible to store $Q$. However, when $Q$ can be written as a sum of tensor products, computing $\exp(tQ)$ becomes feasible by the uniformization method, which does not require explicit storage of $Q$. Results: Here we provide an analogous algorithm for computing $\partial\exp\!(tQ)/\partial\theta$, the differentiated uniformization method. We demonstrate our algorithm for the stochastic SIR model of epidemic spread, for which we show that $Q$ can be written as a sum of tensor products. We estimate monthly infection and recovery rates during the first wave of the COVID-19 pandemic in Austria and quantify their uncertainty in a full Bayesian analysis. Availability: Implementation and data are available at https://github.com/spang-lab/TenSIR.

Machine learning for surface prediction in ACTS

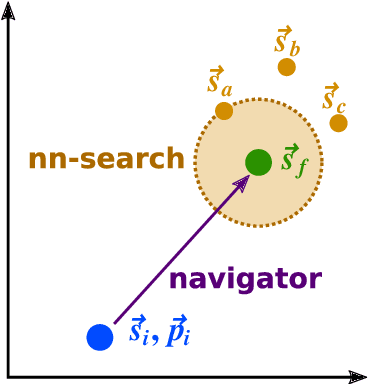
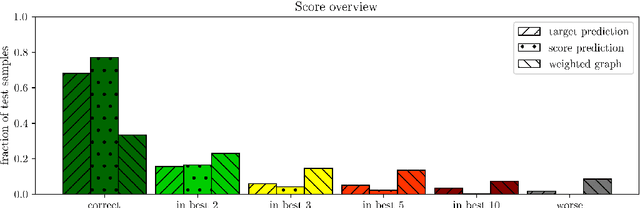
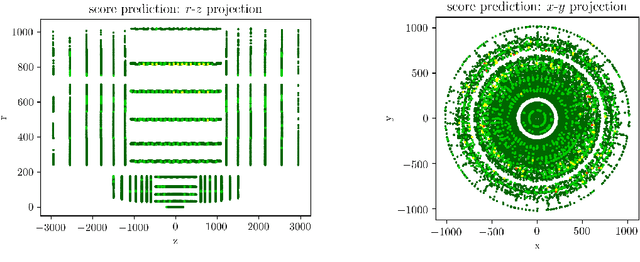
We present an ongoing R&D activity for machine-learning-assisted navigation through detectors to be used for track reconstruction. We investigate different approaches of training neural networks for surface prediction and compare their results. This work is carried out in the context of the ACTS tracking toolkit.