Tiago Santos
Surfacing Estimation Uncertainty in the Decay Parameters of Hawkes Processes with Exponential Kernels
Apr 02, 2021
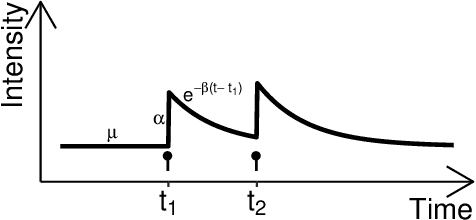
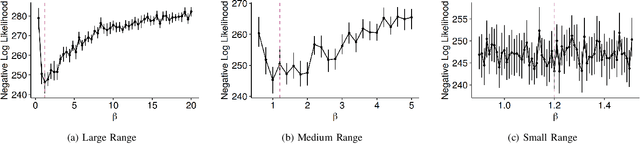
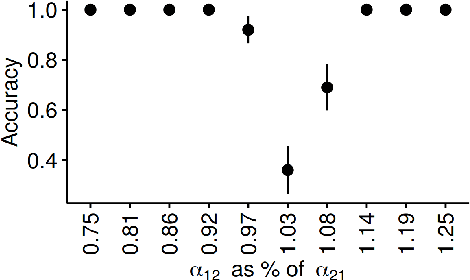
Abstract:As a tool for capturing irregular temporal dependencies (rather than resorting to binning temporal observations to construct time series), Hawkes processes with exponential decay have seen widespread adoption across many application domains, such as predicting the occurrence time of the next earthquake or stock market spike. However, practical applications of Hawkes processes face a noteworthy challenge: There is substantial and often unquantified variance in decay parameter estimations, especially in the case of a small number of observations or when the dynamics behind the observed data suddenly change. We empirically study the cause of these practical challenges and we develop an approach to surface and thereby mitigate them. In particular, our inspections of the Hawkes process likelihood function uncover the properties of the uncertainty when fitting the decay parameter. We thus propose to explicitly capture this uncertainty within a Bayesian framework. With a series of experiments with synthetic and real-world data from domains such as "classical" earthquake modeling or the manifestation of collective emotions on Twitter, we demonstrate that our proposed approach helps to quantify uncertainty and thereby to understand and fit Hawkes processes in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge