Acceptance Rates of Invertible Neural Networks on Electron Spectra from Near-Critical Laser-Plasmas: A Comparison

While the interaction of ultra-intense ultra-short laser pulses with near- and overcritical plasmas cannot be directly observed, experimentally accessible quantities (observables) often only indirectly give information about the underlying plasma dynamics. Furthermore, the information provided by observables is incomplete, making the inverse problem highly ambiguous. Therefore, in order to infer plasma dynamics as well as experimental parameter, the full distribution over parameters given an observation needs to considered, requiring that models are flexible and account for the information lost in the forward process. Invertible Neural Networks (INNs) have been designed to efficiently model both the forward and inverse process, providing the full conditional posterior given a specific measurement. In this work, we benchmark INNs and standard statistical methods on synthetic electron spectra. First, we provide experimental results with respect to the acceptance rate, where our results show increases in acceptance rates up to a factor of 10. Additionally, we show that this increased acceptance rate also results in an increased speed-up for INNs to the same extent. Lastly, we propose a composite algorithm that utilizes INNs and promises low runtimes while preserving high accuracy.

Amortized Bayesian Inference of GISAXS Data with Normalizing Flows

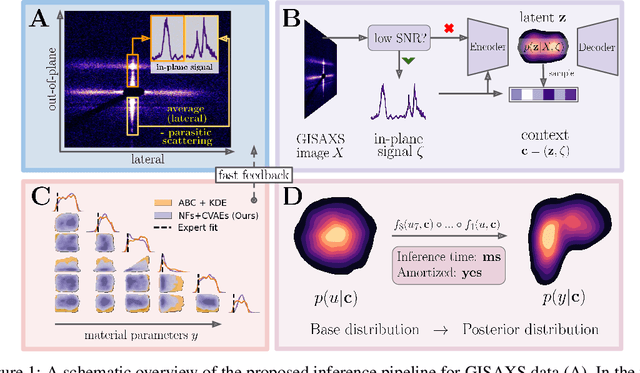
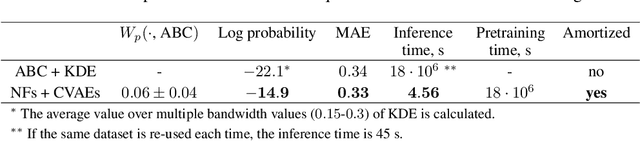
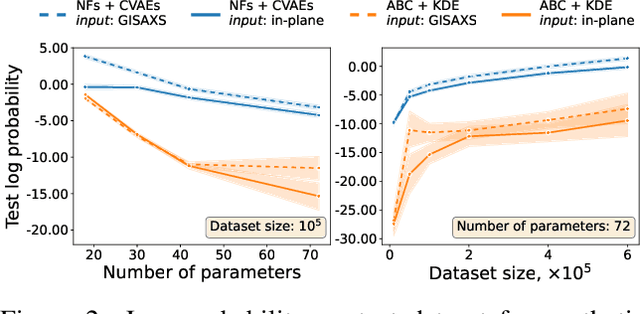
Grazing-Incidence Small-Angle X-ray Scattering (GISAXS) is a modern imaging technique used in material research to study nanoscale materials. Reconstruction of the parameters of an imaged object imposes an ill-posed inverse problem that is further complicated when only an in-plane GISAXS signal is available. Traditionally used inference algorithms such as Approximate Bayesian Computation (ABC) rely on computationally expensive scattering simulation software, rendering analysis highly time-consuming. We propose a simulation-based framework that combines variational auto-encoders and normalizing flows to estimate the posterior distribution of object parameters given its GISAXS data. We apply the inference pipeline to experimental data and demonstrate that our method reduces the inference cost by orders of magnitude while producing consistent results with ABC.