Amortized Bayesian Inference of GISAXS Data with Normalizing Flows

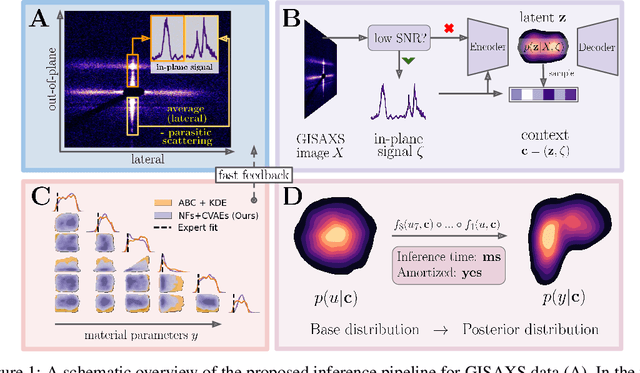
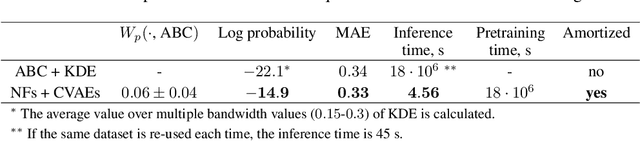
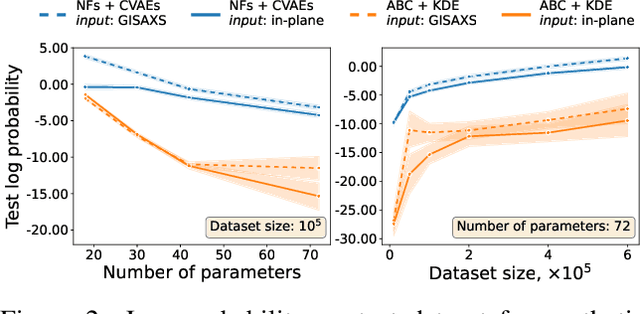
Grazing-Incidence Small-Angle X-ray Scattering (GISAXS) is a modern imaging technique used in material research to study nanoscale materials. Reconstruction of the parameters of an imaged object imposes an ill-posed inverse problem that is further complicated when only an in-plane GISAXS signal is available. Traditionally used inference algorithms such as Approximate Bayesian Computation (ABC) rely on computationally expensive scattering simulation software, rendering analysis highly time-consuming. We propose a simulation-based framework that combines variational auto-encoders and normalizing flows to estimate the posterior distribution of object parameters given its GISAXS data. We apply the inference pipeline to experimental data and demonstrate that our method reduces the inference cost by orders of magnitude while producing consistent results with ABC.

Log-Gaussian processes for AI-assisted TAS experiments

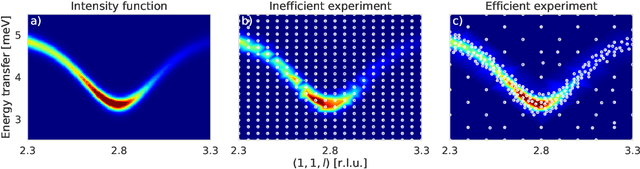
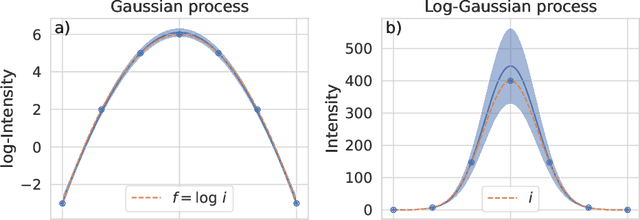
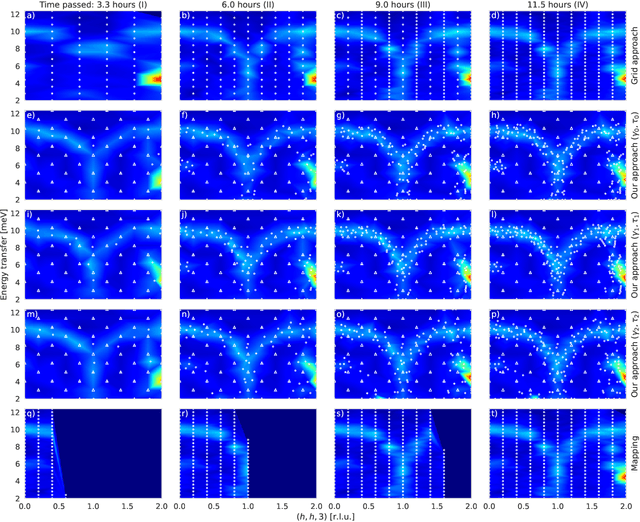
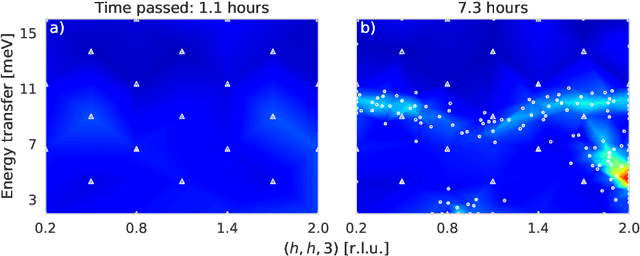
To understand the origins of materials properties, neutron scattering experiments at three-axes spectrometers (TAS) investigate magnetic and lattice excitations in a sample by measuring intensity distributions in its momentum (Q) and energy (E) space. The high demand and limited availability of beam time for TAS experiments however raise the natural question whether we can improve their efficiency or make better use of the experimenter's time. In fact, using TAS, there are a number of scientific questions that require searching for signals of interest in a particular region of Q-E space, but when done manually, it is time consuming and inefficient since the measurement points may be placed in uninformative regions such as the background. Active learning is a promising general machine learning approach that allows to iteratively detect informative regions of signal autonomously, i.e., without human interference, thus avoiding unnecessary measurements and speeding up the experiment. In addition, the autonomous mode allows experimenters to focus on other relevant tasks in the meantime. The approach that we describe in this article exploits log-Gaussian processes which, due to the log transformation, have the largest approximation uncertainties in regions of signal. Maximizing uncertainty as an acquisition function hence directly yields locations for informative measurements. We demonstrate the benefits of our approach on outcomes of a real neutron experiment at the thermal TAS EIGER (PSI) as well as on results of a benchmark in a synthetic setting including numerous different excitations.