Thirupathaiah Vasantam
Quickest Change Detection in the Presence of Transient Adversarial Attacks
Jun 07, 2022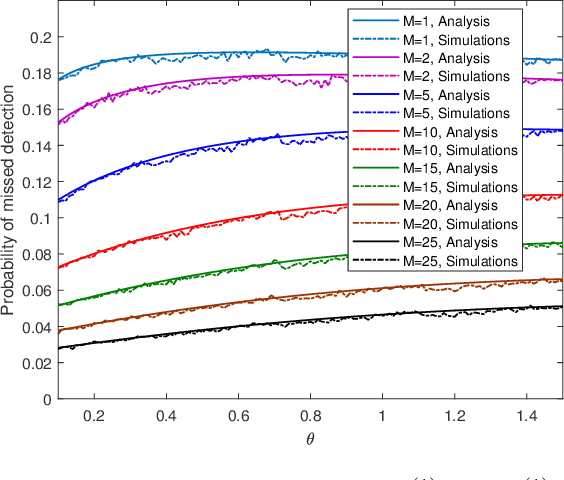
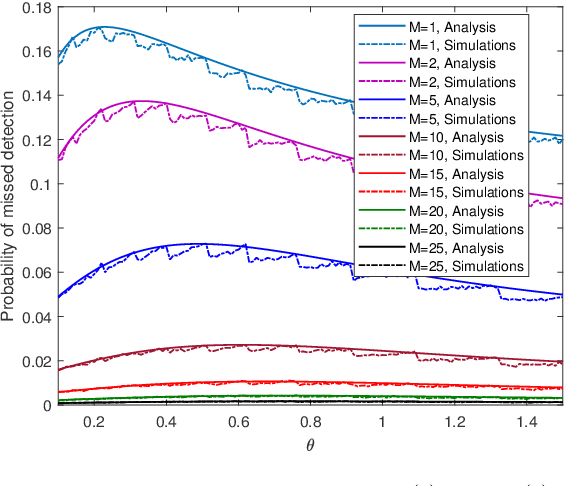
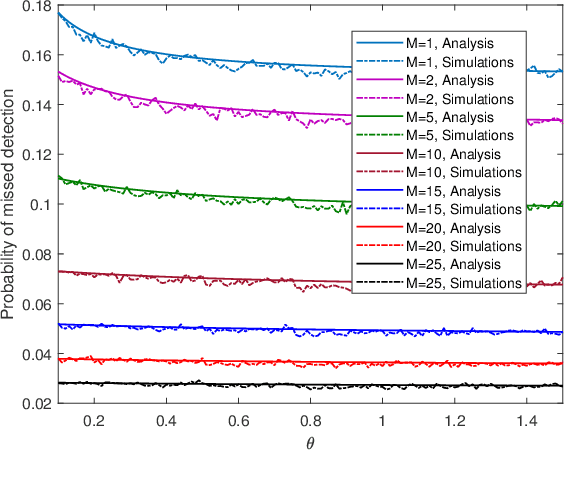
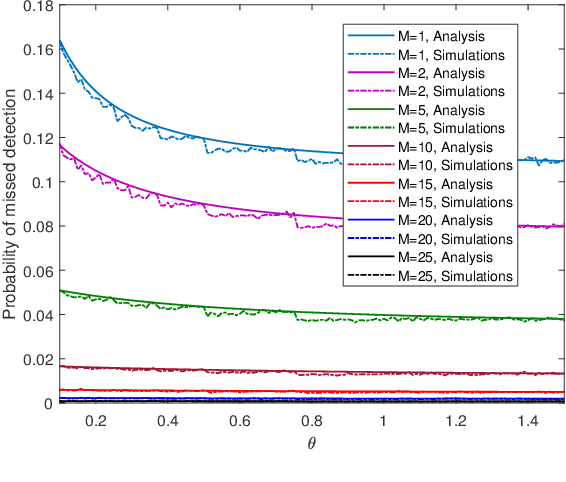
Abstract:We study a monitoring system in which the distributions of sensors' observations change from a nominal distribution to an abnormal distribution in response to an adversary's presence. The system uses the quickest change detection procedure, the Shewhart rule, to detect the adversary that uses its resources to affect the abnormal distribution, so as to hide its presence. The metric of interest is the probability of missed detection within a predefined number of time-slots after the changepoint. Assuming that the adversary's resource constraints are known to the detector, we find the number of required sensors to make the worst-case probability of missed detection less than an acceptable level. The distributions of observations are assumed to be Gaussian, and the presence of the adversary affects their mean. We also provide simulation results to support our analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge