Online Graph Learning via Time-Vertex Adaptive Filters: From Theory to Cardiac Fibrillation

Graph Signal Processing (GSP) provides a powerful framework for analysing complex, interconnected systems by modelling data as signals on graphs. Recent advances in GSP have enabled the learning of graph structures from observed signals, but these methods often struggle with time-varying systems and real-time applications. Adaptive filtering techniques, while effective for online learning, have seen limited application in graph topology estimation from a GSP perspective. To this end, we introduce AdaCGP, an online algorithm for adaptive estimation of the Graph Shift Operator (GSO) from multivariate time series. The GSO is estimated from an adaptive time-vertex autoregressive model through recursive update formulae designed to address sparsity, shift-invariance and bias. Through simulations, we show that AdaCGP performs consistently well across various graph topologies, and achieves improvements in excess of 82% for GSO estimation compared to baseline adaptive vector autoregressive models. In addition, our online variable splitting approach for enforcing sparsity enables near-perfect precision in identifying causal connections while maintaining low false positive rates upon optimisation of the forecast error. Finally, AdaCGP's ability to track changes in graph structure is demonstrated on recordings of ventricular fibrillation dynamics in response to an anti-arrhythmic drug. AdaCGP is shown to be able to identify the stability of critical conduction patterns that may be maintaining the arrhythmia in an intuitive way, together with its potential to support diagnosis and treatment strategies.

Methods of Adaptive Signal Processing on Graphs Using Vertex-Time Autoregressive Models

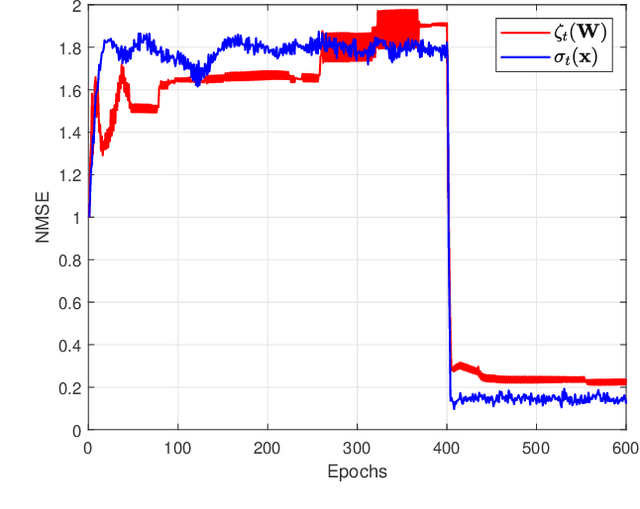
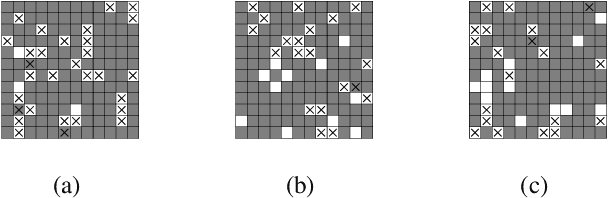
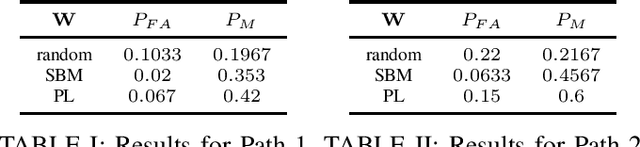
The concept of a random process has been recently extended to graph signals, whereby random graph processes are a class of multivariate stochastic processes whose coefficients are matrices with a \textit{graph-topological} structure. The system identification problem of a random graph process therefore revolves around determining its underlying topology, or mathematically, the graph shift operators (GSOs) i.e. an adjacency matrix or a Laplacian matrix. In the same work that introduced random graph processes, a \textit{batch} optimization method to solve for the GSO was also proposed for the random graph process based on a \textit{causal} vertex-time autoregressive model. To this end, the online version of this optimization problem was proposed via the framework of adaptive filtering. The modified stochastic gradient projection method was employed on the regularized least squares objective to create the filter. The recursion is divided into 3 regularized sub-problems to address issues like multi-convexity, sparsity, commutativity and bias. A discussion on convergence analysis is also included. Finally, experiments are conducted to illustrate the performance of the proposed algorithm, from traditional MSE measure to successful recovery rate regardless correct values, all of which to shed light on the potential, the limit and the possible research attempt of this work.