Accelerated Almost-Sure Convergence Rates for Nonconvex Stochastic Gradient Descent using Stochastic Learning Rates

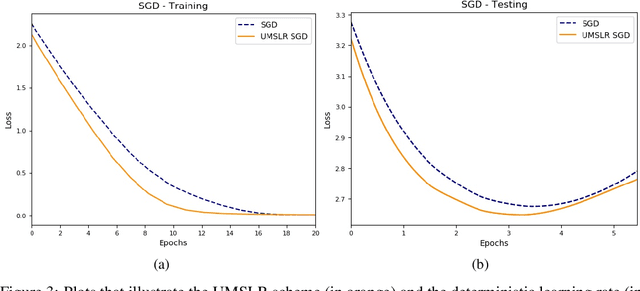
Large-scale optimization problems require algorithms both effective and efficient. One such popular and proven algorithm is Stochastic Gradient Descent which uses first-order gradient information to solve these problems. This paper studies almost-sure convergence rates of the Stochastic Gradient Descent method when instead of deterministic, its learning rate becomes stochastic. In particular, its learning rate is equipped with a multiplicative stochasticity, producing a stochastic learning rate scheme. Theoretical results show accelerated almost-sure convergence rates of Stochastic Gradient Descent in a nonconvex setting when using an appropriate stochastic learning rate, compared to a deterministic-learning-rate scheme. The theoretical results are verified empirically.

Stochastic Learning Rate Optimization in the Stochastic Approximation and Online Learning Settings

In this work, multiplicative stochasticity is applied to the learning rate of stochastic optimization algorithms, giving rise to stochastic learning-rate schemes. In-expectation theoretical convergence results of Stochastic Gradient Descent equipped with this novel stochastic learning rate scheme under the stochastic setting, as well as convergence results under the online optimization settings are provided. Empirical results consider the case of an adaptively uniformly distributed multiplicative stochasticity and include not only Stochastic Gradient Descent, but also other popular algorithms equipped with a stochastic learning rate. They demonstrate noticeable optimization performance gains, with respect to their deterministic-learning-rate versions.