A Transformer-based Math Language Model for Handwritten Math Expression Recognition

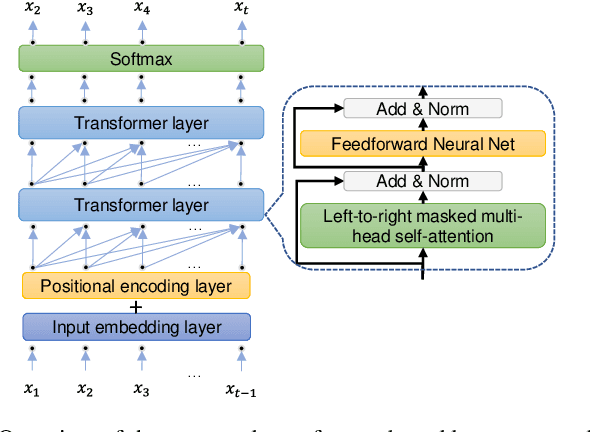
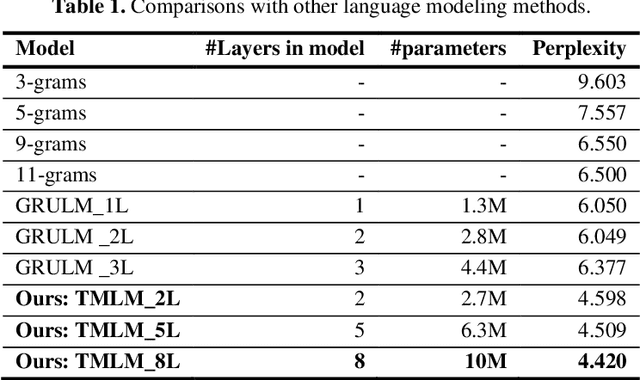
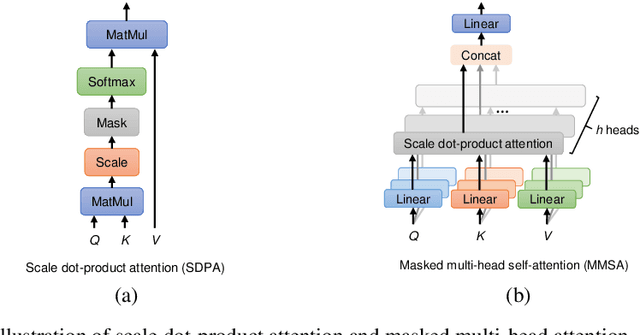
Handwritten mathematical expressions (HMEs) contain ambiguities in their interpretations, even for humans sometimes. Several math symbols are very similar in the writing style, such as dot and comma or 0, O, and o, which is a challenge for HME recognition systems to handle without using contextual information. To address this problem, this paper presents a Transformer-based Math Language Model (TMLM). Based on the self-attention mechanism, the high-level representation of an input token in a sequence of tokens is computed by how it is related to the previous tokens. Thus, TMLM can capture long dependencies and correlations among symbols and relations in a mathematical expression (ME). We trained the proposed language model using a corpus of approximately 70,000 LaTeX sequences provided in CROHME 2016. TMLM achieved the perplexity of 4.42, which outperformed the previous math language models, i.e., the N-gram and recurrent neural network-based language models. In addition, we combine TMLM into a stochastic context-free grammar-based HME recognition system using a weighting parameter to re-rank the top-10 best candidates. The expression rates on the testing sets of CROHME 2016 and CROHME 2019 were improved by 2.97 and 0.83 percentage points, respectively.

Global Context for improving recognition of Online Handwritten Mathematical Expressions

This paper presents a temporal classification method for all three subtasks of symbol segmentation, symbol recognition and relation classification in online handwritten mathematical expressions (HMEs). The classification model is trained by multiple paths of symbols and spatial relations derived from the Symbol Relation Tree (SRT) representation of HMEs. The method benefits from global context of a deep bidirectional Long Short-term Memory network, which learns the temporal classification directly from online handwriting by the Connectionist Temporal Classification loss. To recognize an online HME, a symbol-level parse tree with Context-Free Grammar is constructed, where symbols and spatial relations are obtained from the temporal classification results. We show the effectiveness of the proposed method on the two latest CROHME datasets.

Learning symbol relation tree for online mathematical expression recognition

This paper proposes a method for recognizing online handwritten mathematical expressions (OnHME) by building a symbol relation tree (SRT) directly from a sequence of strokes. A bidirectional recurrent neural network learns from multiple derived paths of SRT to predict both symbols and spatial relations between symbols using global context. The recognition system has two parts: a temporal classifier and a tree connector. The temporal classifier produces an SRT by recognizing an OnHME pattern. The tree connector splits the SRT into several sub-SRTs. The final SRT is formed by looking up the best combination among those sub-SRTs. Besides, we adopt a tree sorting method to deal with various stroke orders. Recognition experiments indicate that the proposed OnHME recognition system is competitive to other methods. The recognition system achieves 44.12% and 41.76% expression recognition rates on the Competition on Recognition of Online Handwritten Mathematical Expressions (CROHME) 2014 and 2016 testing sets.