Marginal Weighted Maximum Log-likelihood for Efficient Learning of Perturb-and-Map models

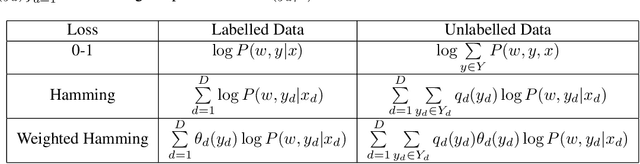
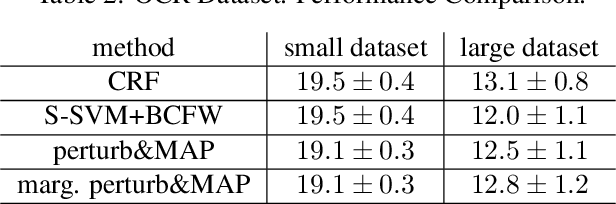
We consider the structured-output prediction problem through probabilistic approaches and generalize the "perturb-and-MAP" framework to more challenging weighted Hamming losses, which are crucial in applications. While in principle our approach is a straightforward marginalization, it requires solving many related MAP inference problems. We show that for log-supermodular pairwise models these operations can be performed efficiently using the machinery of dynamic graph cuts. We also propose to use double stochastic gradient descent, both on the data and on the perturbations, for efficient learning. Our framework can naturally take weak supervision (e.g., partial labels) into account. We conduct a set of experiments on medium-scale character recognition and image segmentation, showing the benefits of our algorithms.

Parameter Learning for Log-supermodular Distributions

We consider log-supermodular models on binary variables, which are probabilistic models with negative log-densities which are submodular. These models provide probabilistic interpretations of common combinatorial optimization tasks such as image segmentation. In this paper, we focus primarily on parameter estimation in the models from known upper-bounds on the intractable log-partition function. We show that the bound based on separable optimization on the base polytope of the submodular function is always inferior to a bound based on "perturb-and-MAP" ideas. Then, to learn parameters, given that our approximation of the log-partition function is an expectation (over our own randomization), we use a stochastic subgradient technique to maximize a lower-bound on the log-likelihood. This can also be extended to conditional maximum likelihood. We illustrate our new results in a set of experiments in binary image denoising, where we highlight the flexibility of a probabilistic model to learn with missing data.