Equation-informed data-driven identification of flow budgets and dynamics

Computational Fluid Dynamics (CFD) is an indispensable method of fluid modelling in engineering applications, reducing the need for physical prototypes and testing for tasks such as design optimisation and performance analysis. Depending on the complexity of the system under consideration, models ranging from low to high fidelity can be used for prediction, allowing significant speed-up. However, the choice of model requires information about the actual dynamics of the flow regime. Correctly identifying the regions/clusters of flow that share the same dynamics has been a challenging research topic to date. In this study, we propose a novel hybrid approach to flow clustering. It consists of characterising each sample point of the system with equation-based features, i.e. features are budgets that represent the contribution of each term from the original governing equation to the local dynamics at each sample point. This was achieved by applying the Sparse Identification of Nonlinear Dynamical systems (SINDy) method pointwise to time evolution data. The method proceeds with equation-based clustering using the Girvan-Newman algorithm. This allows the detection of communities that share the same physical dynamics. The algorithm is implemented in both Eulerian and Lagrangian frameworks. In the Lagrangian, i.e. dynamic approach, the clustering is performed on the trajectory of each point, allowing the change of clusters to be represented also in time. The performance of the algorithm is first tested on a flow around a cylinder. The construction of the dynamic clusters in this test case clearly shows the evolution of the wake from the steady state solution through the transient to the oscillatory solution. Dynamic clustering was then successfully tested on turbulent flow data. Two distinct and well-defined clusters were identified and their temporal evolution was reconstructed.

RONAALP: Reduced-Order Nonlinear Approximation with Active Learning Procedure

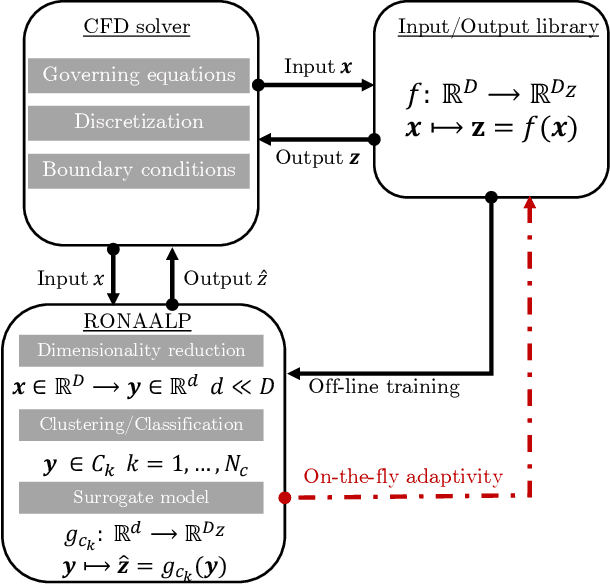
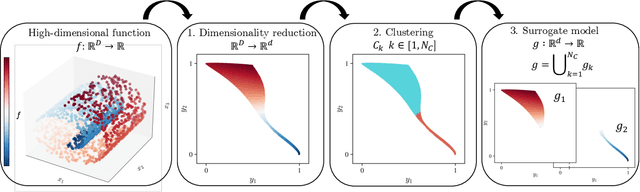
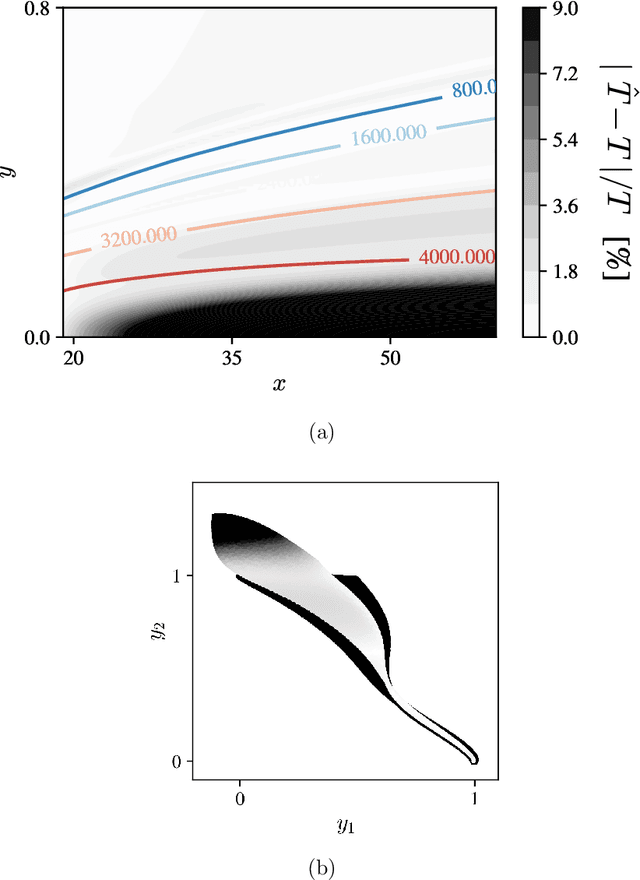
Many engineering applications rely on the evaluation of expensive, non-linear high-dimensional functions. In this paper, we propose the RONAALP algorithm (Reduced Order Nonlinear Approximation with Active Learning Procedure) to incrementally learn a fast and accurate reduced-order surrogate model of a target function on-the-fly as the application progresses. First, the combination of nonlinear auto-encoder, community clustering and radial basis function networks allows to learn an efficient and compact surrogate model with limited training data. Secondly, the active learning procedure overcome any extrapolation issue when evaluating the surrogate model outside of its initial training range during the online stage. This results in generalizable, fast and accurate reduced-order models of high-dimensional functions. The method is demonstrated on three direct numerical simulations of hypersonic flows in chemical nonequilibrium. Accurate simulations of these flows rely on detailed thermochemical gas models that dramatically increase the cost of such calculations. Using RONAALP to learn a reduced-order thermodynamic model surrogate on-the-fly, the cost of such simulation was reduced by up to 75% while maintaining an error of less than 10% on relevant quantities of interest.

Mori-Zwanzig latent space Koopman closure for nonlinear autoencoder

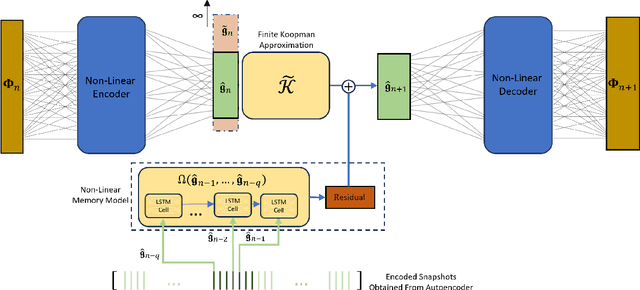
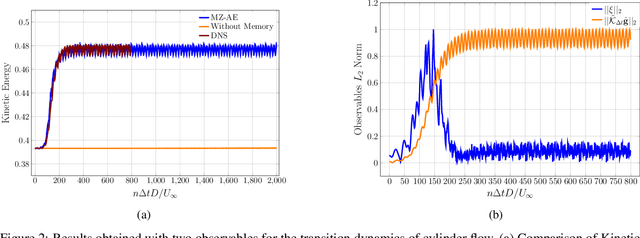
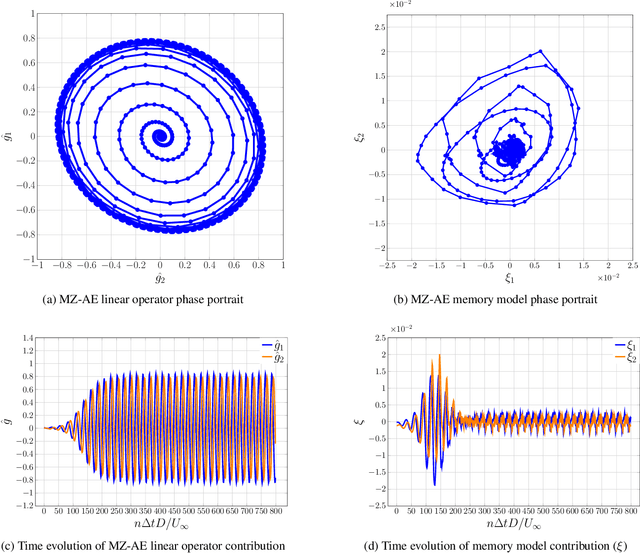
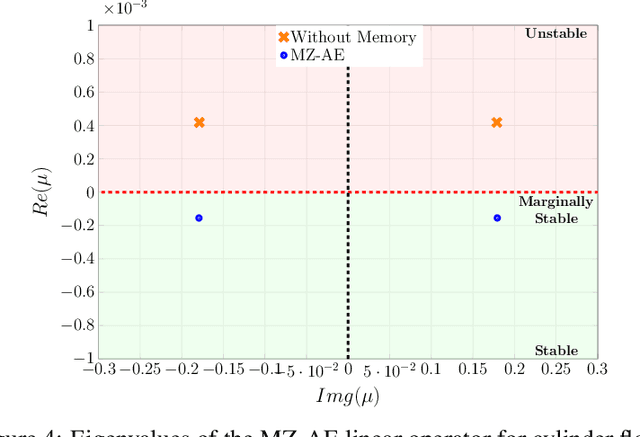
The Koopman operator presents an attractive approach to achieve global linearization of nonlinear systems, making it a valuable method for simplifying the understanding of complex dynamics. While data-driven methodologies have exhibited promise in approximating finite Koopman operators, they grapple with various challenges, such as the judicious selection of observables, dimensionality reduction, and the ability to predict complex system behaviours accurately. This study presents a novel approach termed Mori-Zwanzig autoencoder (MZ-AE) to robustly approximate the Koopman operator in low-dimensional spaces. The proposed method leverages a nonlinear autoencoder to extract key observables for approximating a finite invariant Koopman subspace and integrates a non-Markovian correction mechanism using the Mori-Zwanzig formalism. Consequently, this approach yields a closed representation of dynamics within the latent manifold of the nonlinear autoencoder, thereby enhancing the precision and stability of the Koopman operator approximation. Demonstrations showcase the technique's ability to capture regime transitions in the flow around a circular cylinder. It also provided a low dimensional approximation for chaotic Kuramoto-Sivashinsky with promising short-term predictability and robust long-term statistical performance. By bridging the gap between data-driven techniques and the mathematical foundations of Koopman theory, MZ-AE offers a promising avenue for improved understanding and prediction of complex nonlinear dynamics.

Data-driven framework for input/output lookup tables reduction -- with application to hypersonic flows in chemical non-equilibrium

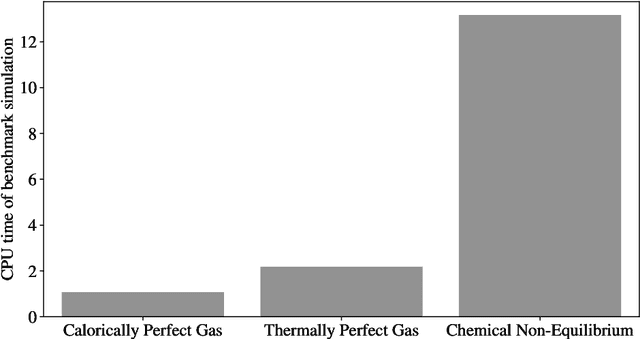
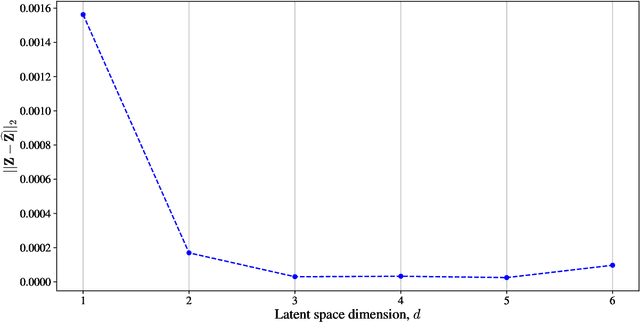
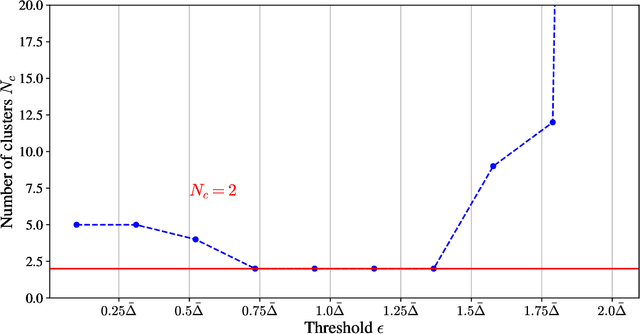
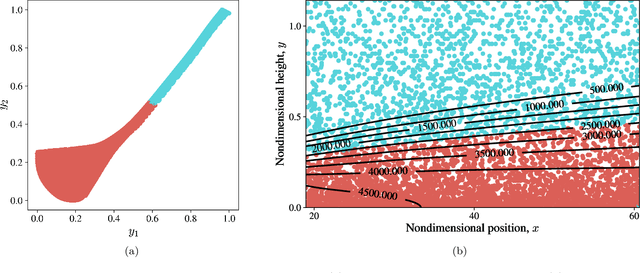
In this paper, we present a novel model-agnostic machine learning technique to extract a reduced thermochemical model for reacting hypersonic flows simulation. A first simulation gathers all relevant thermodynamic states and the corresponding gas properties via a given model. The states are embedded in a low-dimensional space and clustered to identify regions with different levels of thermochemical (non)-equilibrium. Then, a surrogate surface from the reduced cluster-space to the output space is generated using radial-basis-function networks. The method is validated and benchmarked on a simulation of a hypersonic flat-plate boundary layer with finite-rate chemistry. The gas properties of the reactive air mixture are initially modeled using the open-source Mutation++ library. Substituting Mutation++ with the light-weight, machine-learned alternative improves the performance of the solver by 50% while maintaining overall accuracy.

Symmetry-Aware Autoencoders: s-PCA and s-nlPCA

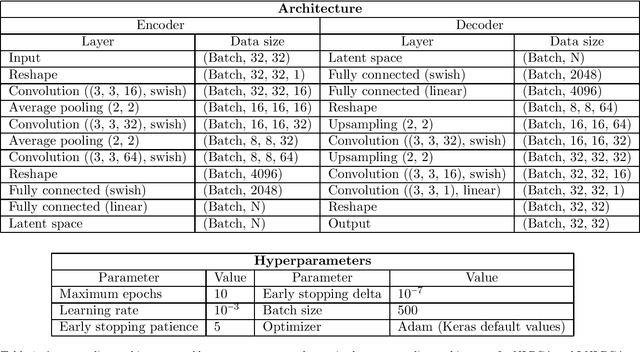
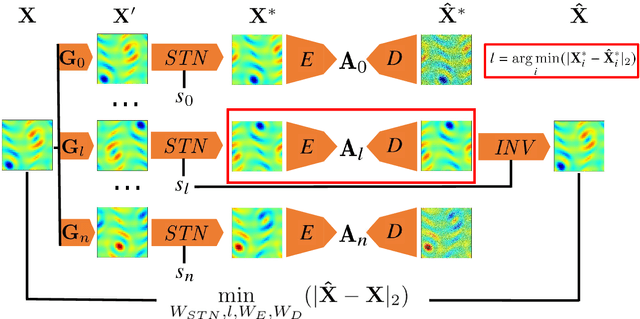
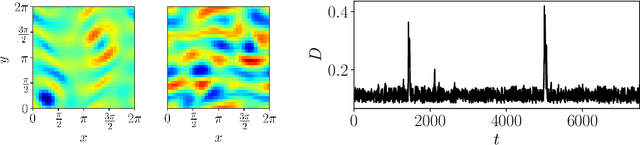
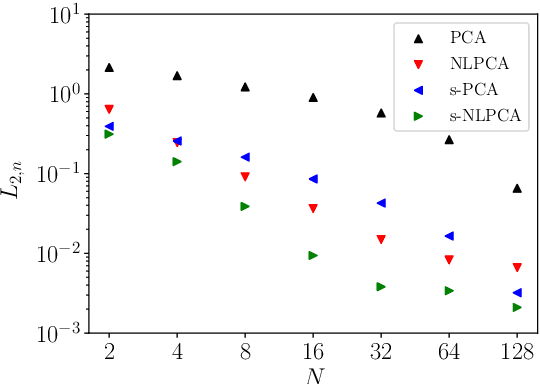
Nonlinear principal component analysis (nlPCA) via autoencoders has attracted attention in the dynamical systems community due to its larger compression rate when compared to linear principal component analysis (PCA). These model reduction methods experience an increase in the dimensionality of the latent space when applied to datasets that exhibit globally invariant samples due to the presence of symmetries. In this study, we introduce a novel machine learning embedding in the autoencoder, which uses spatial transformer networks and Siamese networks to account for continuous and discrete symmetries, respectively. The spatial transformer network discovers the optimal shift for the continuous translation or rotation so that invariant samples are aligned in the periodic directions. Similarly, the Siamese networks collapse samples that are invariant under discrete shifts and reflections. Thus, the proposed symmetry-aware autoencoder is invariant to predetermined input transformations dictating the dynamics of the underlying physical system. This embedding can be employed with both linear and nonlinear reduction methods, which we term symmetry-aware PCA (s-PCA) and symmetry-aware nlPCA (s-nlPCA). We apply the proposed framework to 3 fluid flow problems: Burgers' equation, the simulation of the flow through a step diffuser and the Kolmogorov flow to showcase the capabilities for cases exhibiting only continuous symmetries, only discrete symmetries or a combination of both.