MAUCell: An Adaptive Multi-Attention Framework for Video Frame Prediction

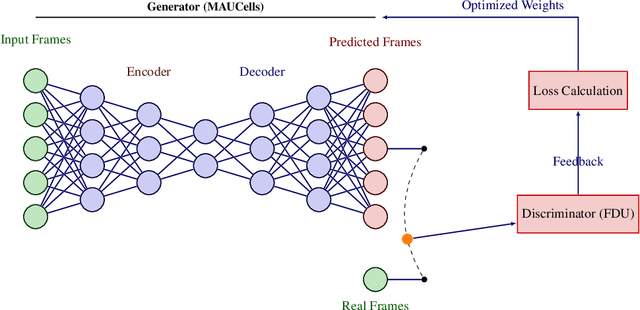
Temporal sequence modeling stands as the fundamental foundation for video prediction systems and real-time forecasting operations as well as anomaly detection applications. The achievement of accurate predictions through efficient resource consumption remains an ongoing issue in contemporary temporal sequence modeling. We introduce the Multi-Attention Unit (MAUCell) which combines Generative Adversarial Networks (GANs) and spatio-temporal attention mechanisms to improve video frame prediction capabilities. Our approach implements three types of attention models to capture intricate motion sequences. A dynamic combination of these attention outputs allows the model to reach both advanced decision accuracy along with superior quality while remaining computationally efficient. The integration of GAN elements makes generated frames appear more true to life therefore the framework creates output sequences which mimic real-world footage. The new design system maintains equilibrium between temporal continuity and spatial accuracy to deliver reliable video prediction. Through a comprehensive evaluation methodology which merged the perceptual LPIPS measurement together with classic tests MSE, MAE, SSIM and PSNR exhibited enhancing capabilities than contemporary approaches based on direct benchmark tests of Moving MNIST, KTH Action, and CASIA-B (Preprocessed) datasets. Our examination indicates that MAUCell shows promise for operational time requirements. The research findings demonstrate how GANs work best with attention mechanisms to create better applications for predicting video sequences.

Mori-Zwanzig latent space Koopman closure for nonlinear autoencoder

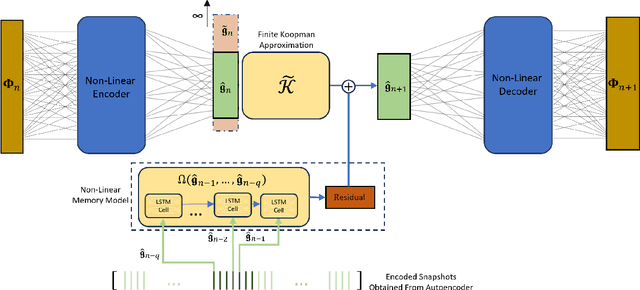
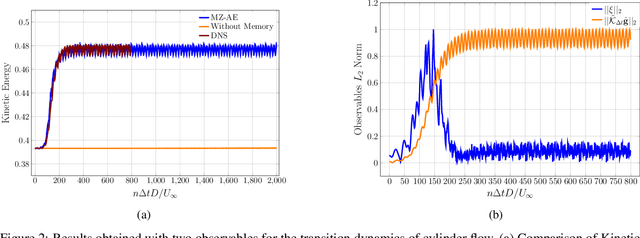
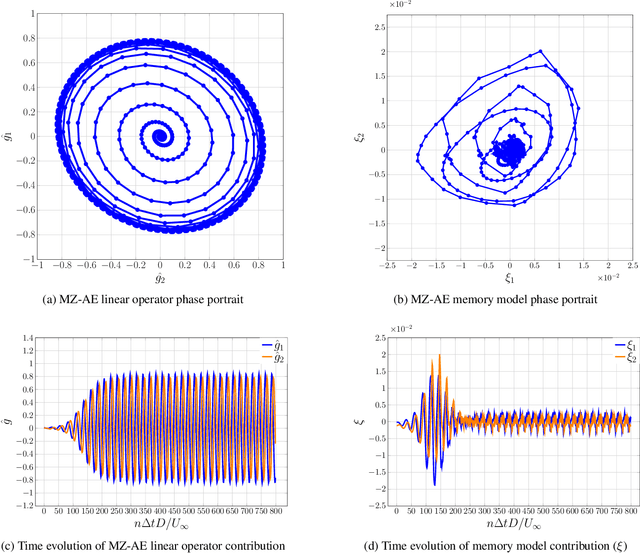
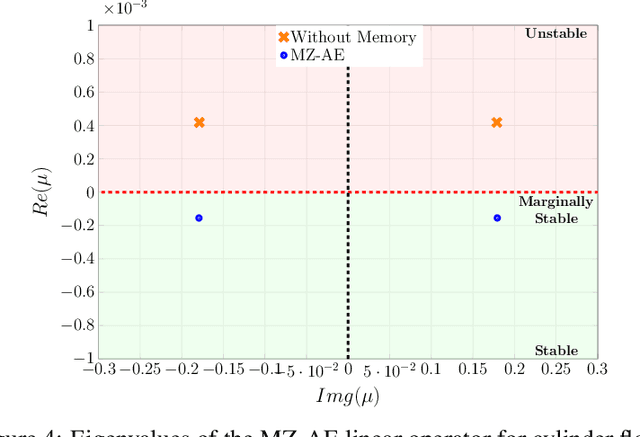
The Koopman operator presents an attractive approach to achieve global linearization of nonlinear systems, making it a valuable method for simplifying the understanding of complex dynamics. While data-driven methodologies have exhibited promise in approximating finite Koopman operators, they grapple with various challenges, such as the judicious selection of observables, dimensionality reduction, and the ability to predict complex system behaviours accurately. This study presents a novel approach termed Mori-Zwanzig autoencoder (MZ-AE) to robustly approximate the Koopman operator in low-dimensional spaces. The proposed method leverages a nonlinear autoencoder to extract key observables for approximating a finite invariant Koopman subspace and integrates a non-Markovian correction mechanism using the Mori-Zwanzig formalism. Consequently, this approach yields a closed representation of dynamics within the latent manifold of the nonlinear autoencoder, thereby enhancing the precision and stability of the Koopman operator approximation. Demonstrations showcase the technique's ability to capture regime transitions in the flow around a circular cylinder. It also provided a low dimensional approximation for chaotic Kuramoto-Sivashinsky with promising short-term predictability and robust long-term statistical performance. By bridging the gap between data-driven techniques and the mathematical foundations of Koopman theory, MZ-AE offers a promising avenue for improved understanding and prediction of complex nonlinear dynamics.