Taozeng Zhu
Optimize-via-Predict: Realizing out-of-sample optimality in data-driven optimization
Sep 20, 2023


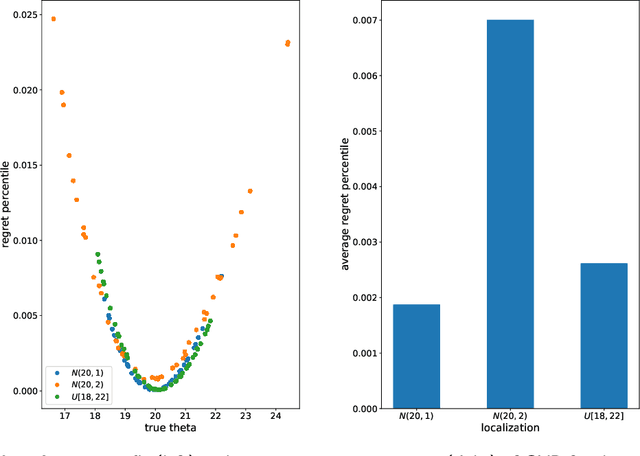
Abstract:We examine a stochastic formulation for data-driven optimization wherein the decision-maker is not privy to the true distribution, but has knowledge that it lies in some hypothesis set and possesses a historical data set, from which information about it can be gleaned. We define a prescriptive solution as a decision rule mapping such a data set to decisions. As there does not exist prescriptive solutions that are generalizable over the entire hypothesis set, we define out-of-sample optimality as a local average over a neighbourhood of hypotheses, and averaged over the sampling distribution. We prove sufficient conditions for local out-of-sample optimality, which reduces to functions of the sufficient statistic of the hypothesis family. We present an optimization problem that would solve for such an out-of-sample optimal solution, and does so efficiently by a combination of sampling and bisection search algorithms. Finally, we illustrate our model on the newsvendor model, and find strong performance when compared against alternatives in the literature. There are potential implications of our research on end-to-end learning and Bayesian optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge