JITuNE: Just-In-Time Hyperparameter Tuning for Network Embedding Algorithms

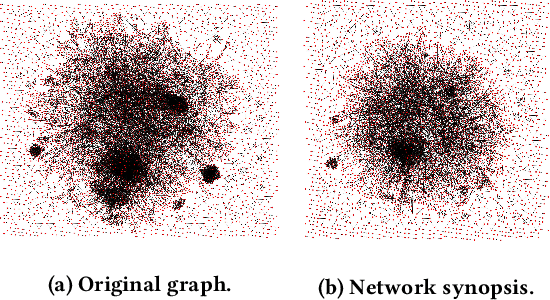
Network embedding (NE) can generate succinct node representations for massive-scale networks and enable direct applications of common machine learning methods to the network structure. Various NE algorithms have been proposed and used in a number of applications, such as node classification and link prediction. NE algorithms typically contain hyperparameters that are key to performance, but the hyperparameter tuning process can be time consuming. It is desirable to have the hyperparameters tuned within a specified length of time. Although AutoML methods have been applied to the hyperparameter tuning of NE algorithms, the problem of how to tune hyperparameters in a given period of time is not studied for NE algorithms before. In this paper, we propose JITuNE, a just-in-time hyperparameter tuning framework for NE algorithms. Our JITuNE framework enables the time-constrained hyperparameter tuning for NE algorithms by employing the tuning over hierarchical network synopses and transferring the knowledge obtained on synopses to the whole network. The hierarchical generation of synopsis and a time-constrained tuning method enable the constraining of overall tuning time. Extensive experiments demonstrate that JITuNE can significantly improve performances of NE algorithms, outperforming state-of-the-art methods within the same number of algorithm runs.

Variance Suppression: Balanced Training Process in Deep Learning

Stochastic gradient descent updates parameters with summation gradient computed from a random data batch. This summation will lead to unbalanced training process if the data we obtained is unbalanced. To address this issue, this paper takes the error variance and error mean both into consideration. The adaptively adjusting approach of two terms trading off is also given in our algorithm. Due to this algorithm can suppress error variance, we named it Variance Suppression Gradient Descent (VSSGD). Experimental results have demonstrated that VSSGD can accelerate the training process, effectively prevent overfitting, improve the networks learning capacity from small samples.