Accurate and robust Shapley Values for explaining predictions and focusing on local important variables

Although Shapley Values (SV) are widely used in explainable AI, they can be poorly understood and estimated, which implies that their analysis may lead to spurious inferences and explanations. As a starting point, we remind an invariance principle for SV and derive the correct approach for computing the SV of categorical variables that are particularly sensitive to the encoding used. In the case of tree-based models, we introduce two estimators of Shapley Values that exploit efficiently the tree structure and are more accurate than state-of-the-art methods. For interpreting additive explanations, we recommend to filter the non-influential variables and to compute the Shapley Values only for groups of influential variables. For this purpose, we use the concept of "Same Decision Probability" (SDP) that evaluates the robustness of a prediction when some variables are missing. This prior selection procedure produces sparse additive explanations easier to visualize and analyse. Simulations and comparisons are performed with state-of-the-art algorithm, and show the practical gain of our approach.

The Shapley Value of coalition of variables provides better explanations

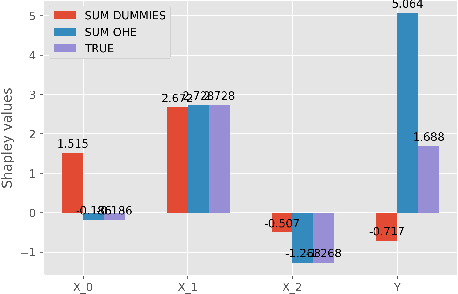
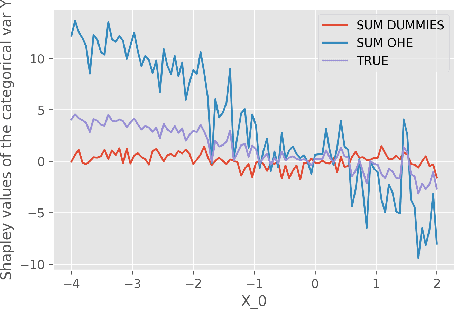
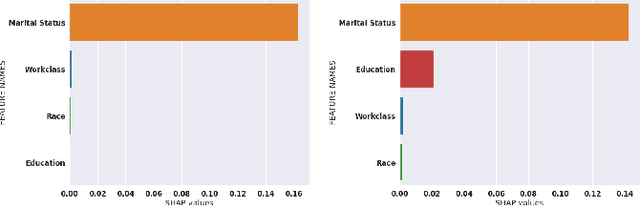
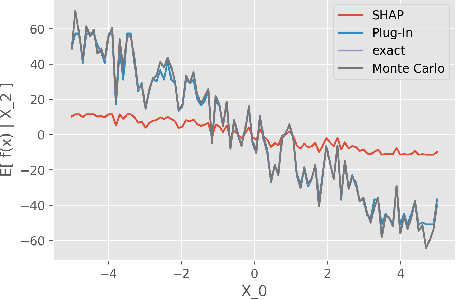
While Shapley Values (SV) are one of the gold standard for interpreting machine learning models, we show that they are still poorly understood, in particular in the presence of categorical variables or of variables of low importance. For instance, we show that the popular practice that consists in summing the SV of dummy variables is false as it provides wrong estimates of all the SV in the model and implies spurious interpretations. Based on the identification of null and active coalitions, and a coalitional version of the SV, we provide a correct computation and inference of important variables. Moreover, a Python library (All the experiments and simulations can be reproduced with the publicly available library Active Coalition of Variables, https://www.github.com/salimamoukou/acv00) that computes reliably conditional expectations and SV for tree-based models, is implemented and compared with state-of-the-art algorithms on toy models and real data sets.