Combining haplotypers

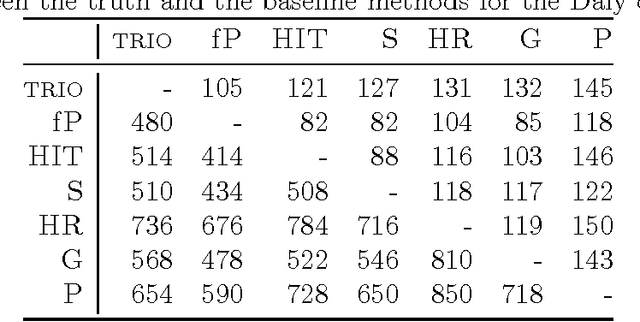
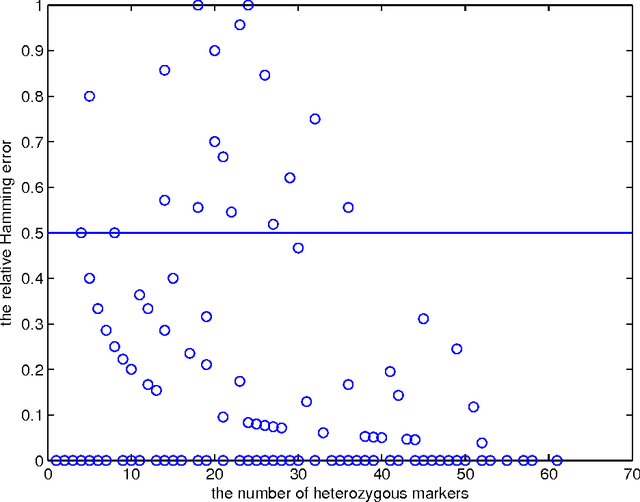
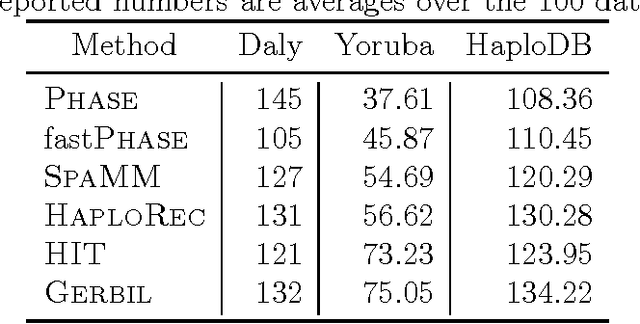
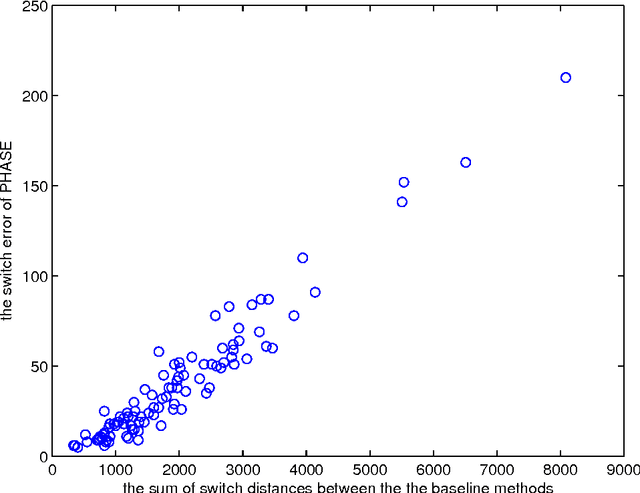
Statistically resolving the underlying haplotype pair for a genotype measurement is an important intermediate step in gene mapping studies, and has received much attention recently. Consequently, a variety of methods for this problem have been developed. Different methods employ different statistical models, and thus implicitly encode different assumptions about the nature of the underlying haplotype structure. Depending on the population sample in question, their relative performance can vary greatly, and it is unclear which method to choose for a particular sample. Instead of choosing a single method, we explore combining predictions returned by different methods in a principled way, and thereby circumvent the problem of method selection. We propose several techniques for combining haplotype reconstructions and analyze their computational properties. In an experimental study on real-world haplotype data we show that such techniques can provide more accurate and robust reconstructions, and are useful for outlier detection. Typically, the combined prediction is at least as accurate as or even more accurate than the best individual method, effectively circumventing the method selection problem.

Summarization Techniques for Pattern Collections in Data Mining

Discovering patterns from data is an important task in data mining. There exist techniques to find large collections of many kinds of patterns from data very efficiently. A collection of patterns can be regarded as a summary of the data. A major difficulty with patterns is that pattern collections summarizing the data well are often very large. In this dissertation we describe methods for summarizing pattern collections in order to make them also more understandable. More specifically, we focus on the following themes: 1) Quality value simplifications. 2) Pattern orderings. 3) Pattern chains and antichains. 4) Change profiles. 5) Inverse pattern discovery.

The Computational Complexity of Orientation Search Problems in Cryo-Electron Microscopy

In this report we study the problem of determining three-dimensional orientations for noisy projections of randomly oriented identical particles. The problem is of central importance in the tomographic reconstruction of the density map of macromolecular complexes from electron microscope images and it has been studied intensively for more than 30 years. We analyze the computational complexity of the orientation problem and show that while several variants of the problem are $NP$-hard, inapproximable and fixed-parameter intractable, some restrictions are polynomial-time approximable within a constant factor or even solvable in logarithmic space. The orientation search problem is formalized as a constrained line arrangement problem that is of independent interest. The negative complexity results give a partial justification for the heuristic methods used in orientation search, and the positive complexity results on the orientation search have some positive implications also to the problem of finding functionally analogous genes. A preliminary version ``The Computational Complexity of Orientation Search in Cryo-Electron Microscopy'' appeared in Proc. ICCS 2004, LNCS 3036, pp. 231--238. Springer-Verlag 2004.