Adapter Merging with Centroid Prototype Mapping for Scalable Class-Incremental Learning

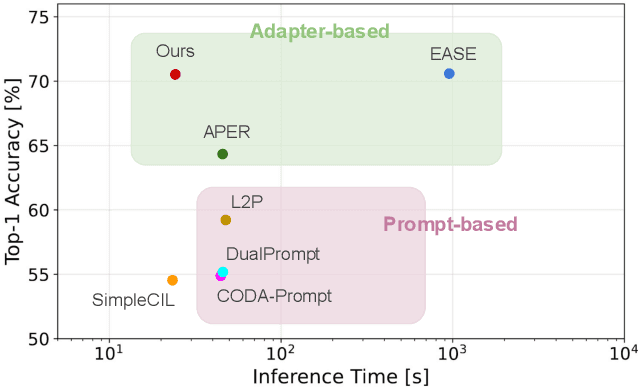
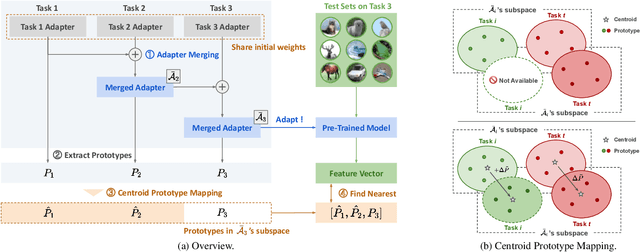
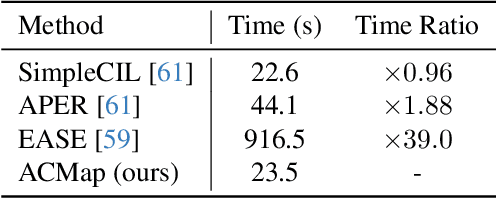
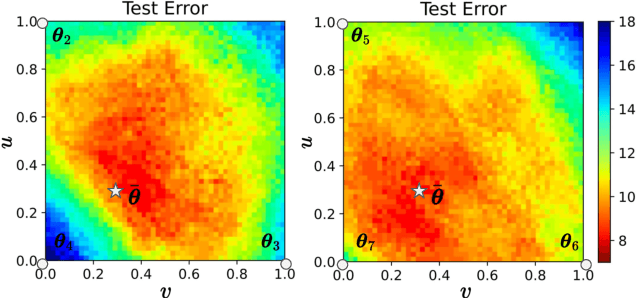
We propose Adapter Merging with Centroid Prototype Mapping (ACMap), an exemplar-free framework for class-incremental learning (CIL) that addresses both catastrophic forgetting and scalability. While existing methods trade-off between inference time and accuracy, ACMap consolidates task-specific adapters into a single adapter, ensuring constant inference time across tasks without compromising accuracy. The framework employs adapter merging to build a shared subspace that aligns task representations and mitigates forgetting, while centroid prototype mapping maintains high accuracy through consistent adaptation in the shared subspace. To further improve scalability, an early stopping strategy limits adapter merging as tasks increase. Extensive experiments on five benchmark datasets demonstrate that ACMap matches state-of-the-art accuracy while maintaining inference time comparable to the fastest existing methods. The code is available at https://github.com/tf63/ACMap

On the Limitation of Diffusion Models for Synthesizing Training Datasets

Synthetic samples from diffusion models are promising for leveraging in training discriminative models as replications of real training datasets. However, we found that the synthetic datasets degrade classification performance over real datasets even when using state-of-the-art diffusion models. This means that modern diffusion models do not perfectly represent the data distribution for the purpose of replicating datasets for training discriminative tasks. This paper investigates the gap between synthetic and real samples by analyzing the synthetic samples reconstructed from real samples through the diffusion and reverse process. By varying the time steps starting the reverse process in the reconstruction, we can control the trade-off between the information in the original real data and the information added by diffusion models. Through assessing the reconstructed samples and trained models, we found that the synthetic data are concentrated in modes of the training data distribution as the reverse step increases, and thus, they are difficult to cover the outer edges of the distribution. Our findings imply that modern diffusion models are insufficient to replicate training data distribution perfectly, and there is room for the improvement of generative modeling in the replication of training datasets.