Hierarchical Multi-Agent Reinforcement Learning for Assessing False-Data Injection Attacks on Transportation Networks

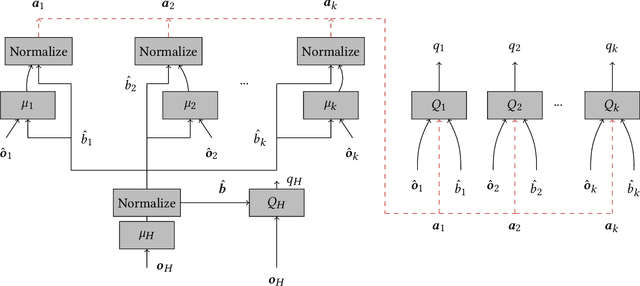
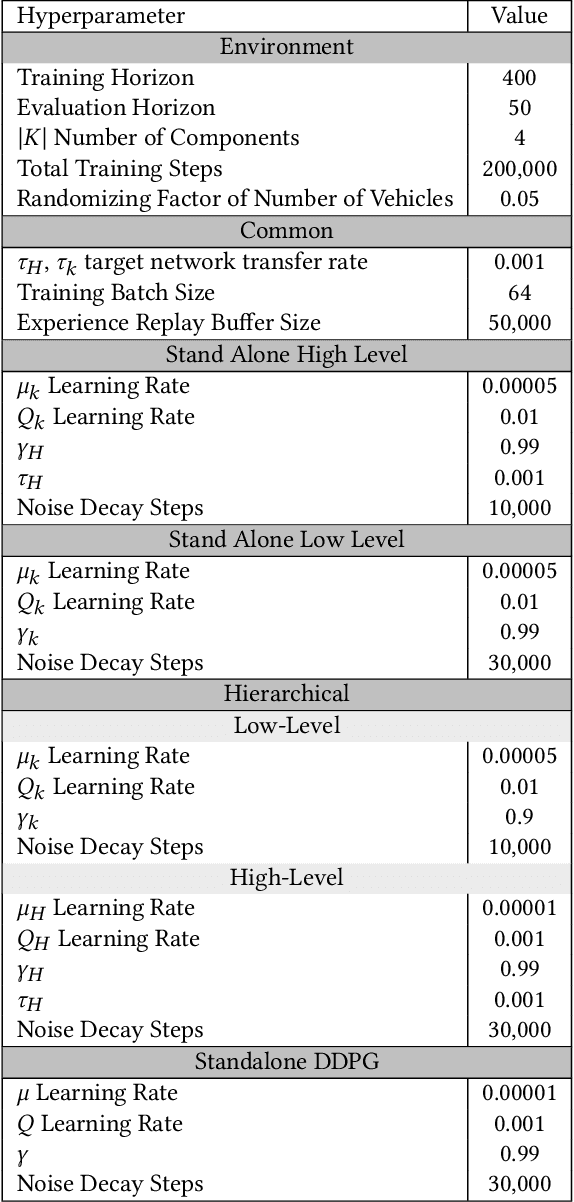
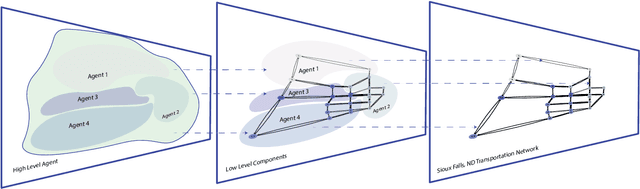
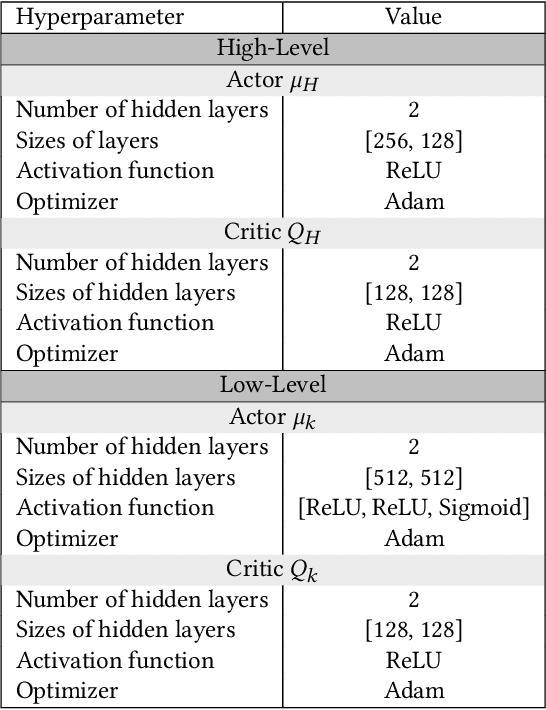
The increasing reliance of drivers on navigation applications has made transportation networks more susceptible to data-manipulation attacks by malicious actors. Adversaries may exploit vulnerabilities in the data collection or processing of navigation services to inject false information, and to thus interfere with the drivers' route selection. Such attacks can significantly increase traffic congestions, resulting in substantial waste of time and resources, and may even disrupt essential services that rely on road networks. To assess the threat posed by such attacks, we introduce a computational framework to find worst-case data-injection attacks against transportation networks. First, we devise an adversarial model with a threat actor who can manipulate drivers by increasing the travel times that they perceive on certain roads. Then, we employ hierarchical multi-agent reinforcement learning to find an approximate optimal adversarial strategy for data manipulation. We demonstrate the applicability of our approach through simulating attacks on the Sioux Falls, ND network topology.

Deep Reinforcement Learning based Adaptive Moving Target Defense

Moving target defense (MTD) is a proactive defense approach that aims to thwart attacks by continuously changing the attack surface of a system (e.g., changing host or network configurations), thereby increasing the adversary's uncertainty and attack cost. To maximize the impact of MTD, a defender must strategically choose when and what changes to make, taking into account both the characteristics of its system as well as the adversary's observed activities. Finding an optimal strategy for MTD presents a significant challenge, especially when facing a resourceful and determined adversary who may respond to the defender's actions. In this paper, we propose finding optimal MTD strategies using deep reinforcement learning. Based on an established model of adaptive MTD, we formulate finding an MTD strategy as finding a policy for a partially-observable Markov decision process. To significantly improve training performance, we introduce compact memory representations. To demonstrate our approach, we provide thorough numerical results, showing significant improvement over existing strategies.