Improving self-training under distribution shifts via anchored confidence with theoretical guarantees

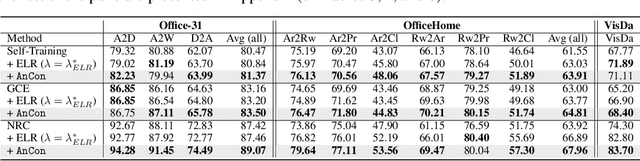
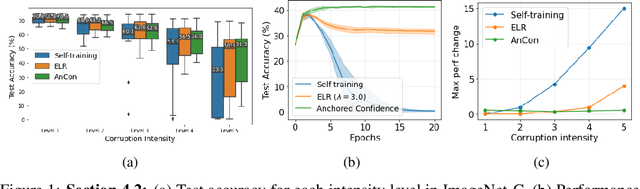
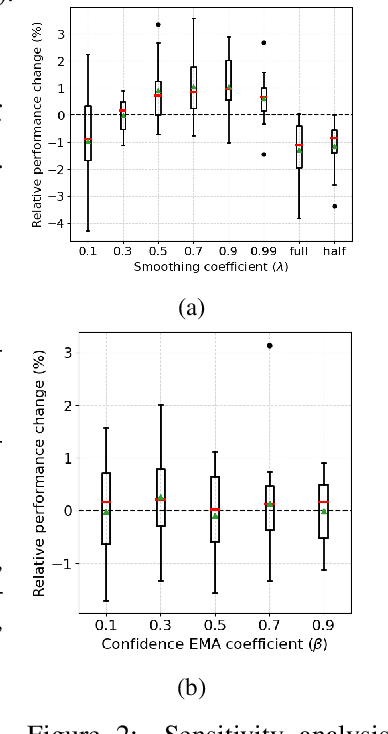
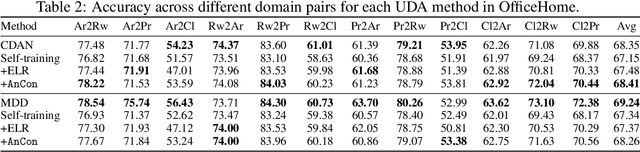
Self-training often falls short under distribution shifts due to an increased discrepancy between prediction confidence and actual accuracy. This typically necessitates computationally demanding methods such as neighborhood or ensemble-based label corrections. Drawing inspiration from insights on early learning regularization, we develop a principled method to improve self-training under distribution shifts based on temporal consistency. Specifically, we build an uncertainty-aware temporal ensemble with a simple relative thresholding. Then, this ensemble smooths noisy pseudo labels to promote selective temporal consistency. We show that our temporal ensemble is asymptotically correct and our label smoothing technique can reduce the optimality gap of self-training. Our extensive experiments validate that our approach consistently improves self-training performances by 8% to 16% across diverse distribution shift scenarios without a computational overhead. Besides, our method exhibits attractive properties, such as improved calibration performance and robustness to different hyperparameter choices.

IW-GAE: Importance weighted group accuracy estimation for improved calibration and model selection in unsupervised domain adaptation

Reasoning about a model's accuracy on a test sample from its confidence is a central problem in machine learning, being connected to important applications such as uncertainty representation, model selection, and exploration. While these connections have been well-studied in the i.i.d. settings, distribution shifts pose significant challenges to the traditional methods. Therefore, model calibration and model selection remain challenging in the unsupervised domain adaptation problem--a scenario where the goal is to perform well in a distribution shifted domain without labels. In this work, we tackle difficulties coming from distribution shifts by developing a novel importance weighted group accuracy estimator. Specifically, we formulate an optimization problem for finding an importance weight that leads to an accurate group accuracy estimation in the distribution shifted domain with theoretical analyses. Extensive experiments show the effectiveness of group accuracy estimation on model calibration and model selection. Our results emphasize the significance of group accuracy estimation for addressing challenges in unsupervised domain adaptation, as an orthogonal improvement direction with improving transferability of accuracy.

Deep Learning Requires Explicit Regularization for Reliable Predictive Probability

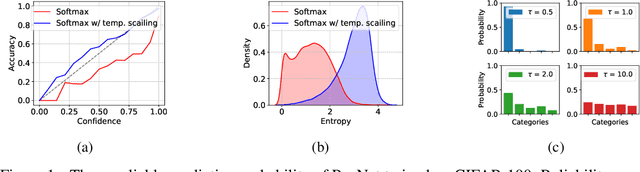
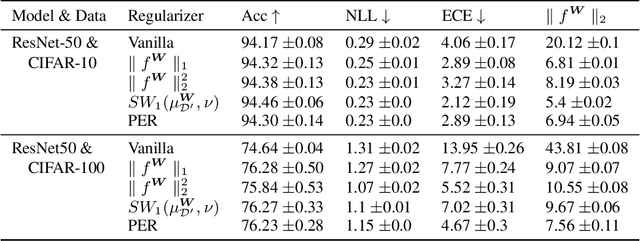
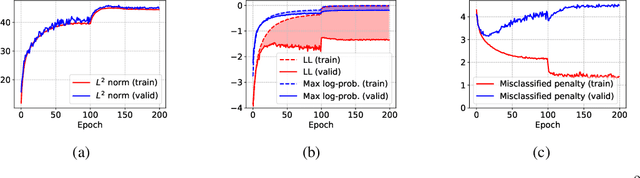
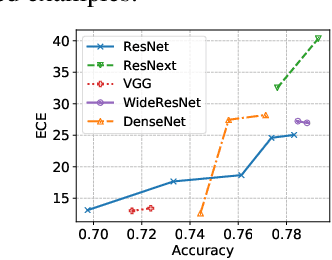
From the statistical learning perspective, complexity control via explicit regularization is a necessity for improving the generalization of over-parameterized models, which deters the memorization of intricate patterns existing only in the training data. However, the impressive generalization performance of over-parameterized neural networks with only implicit regularization challenges this traditional role of explicit regularization. Furthermore, explicit regularization does not prevent neural networks from memorizing unnatural patterns, such as random labels, that cannot be generalized. In this work, we revisit the role and importance of explicit regularization methods for generalizing the predictive probability, not just the generalization of the 0-1 loss. Specifically, we present extensive empirical evidence showing the versatility of explicit regularization techniques on improving the reliability of the predictive probability, which enables better uncertainty representation and prevents the overconfidence problem. Our findings present a new direction to improve the predictive probability quality of deterministic neural networks, unlike the mainstream of approaches concentrates on building stochastic representation with Bayesian neural networks, ensemble methods, and hybrid models.

Being Bayesian about Categorical Probability

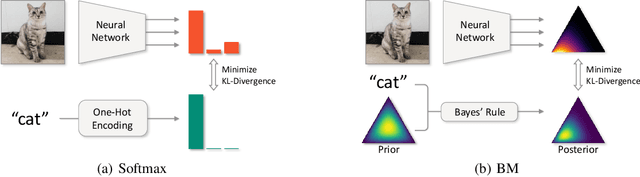
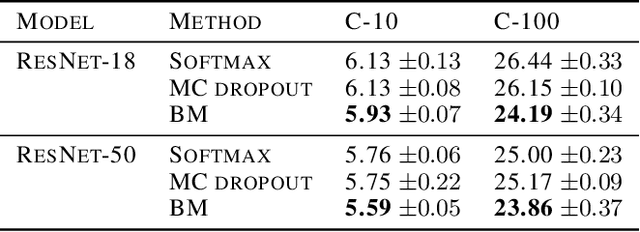
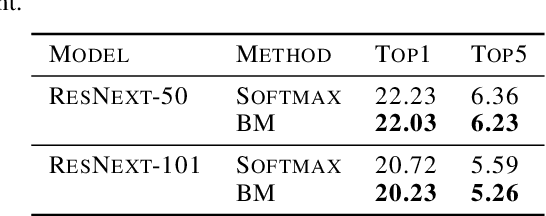
Neural networks utilize the softmax as a building block in classification tasks, which contains an overconfidence problem and lacks an uncertainty representation ability. As a Bayesian alternative to the softmax, we consider a random variable of a categorical probability over class labels. In this framework, the prior distribution explicitly models the presumed noise inherent in the observed label, which provides consistent gains in generalization performance in multiple challenging tasks. The proposed method inherits advantages of Bayesian approaches that achieve better uncertainty estimation and model calibration. Our method can be implemented as a plug-and-play loss function with negligible computational overhead compared to the softmax with the cross-entropy loss function.

Regularizing activations in neural networks via distribution matching with the Wasserstein metric

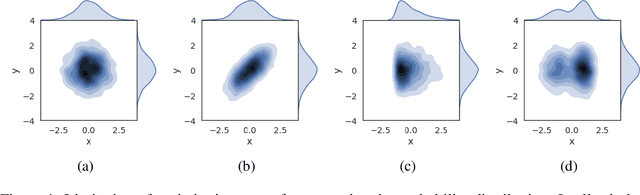
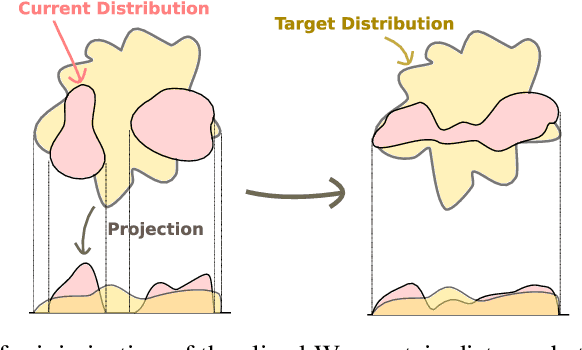
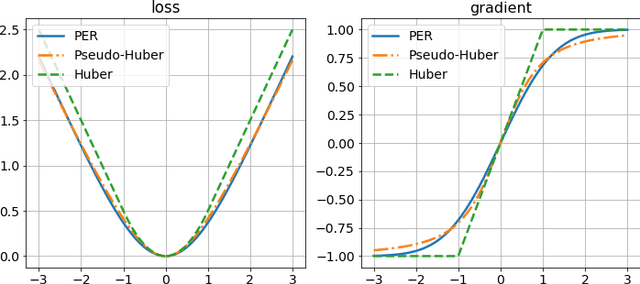
Regularization and normalization have become indispensable components in training deep neural networks, resulting in faster training and improved generalization performance. We propose the projected error function regularization loss (PER) that encourages activations to follow the standard normal distribution. PER randomly projects activations onto one-dimensional space and computes the regularization loss in the projected space. PER is similar to the Pseudo-Huber loss in the projected space, thus taking advantage of both $L^1$ and $L^2$ regularization losses. Besides, PER can capture the interaction between hidden units by projection vector drawn from a unit sphere. By doing so, PER minimizes the upper bound of the Wasserstein distance of order one between an empirical distribution of activations and the standard normal distribution. To the best of the authors' knowledge, this is the first work to regularize activations via distribution matching in the probability distribution space. We evaluate the proposed method on the image classification task and the word-level language modeling task.