Deep Learning Requires Explicit Regularization for Reliable Predictive Probability

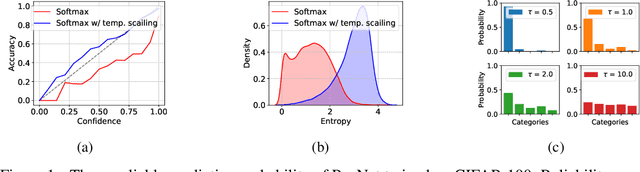
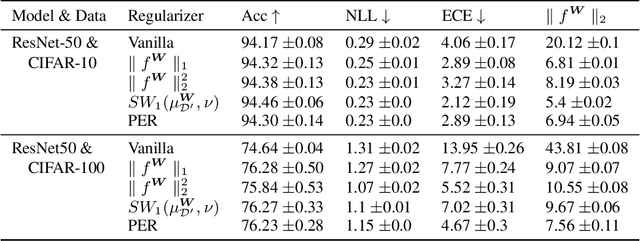
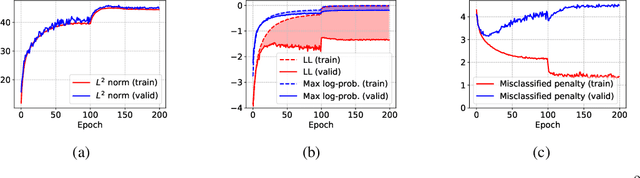
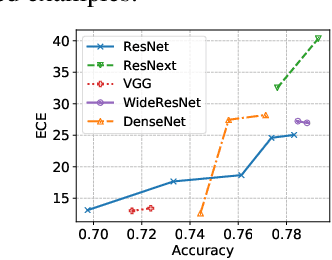
From the statistical learning perspective, complexity control via explicit regularization is a necessity for improving the generalization of over-parameterized models, which deters the memorization of intricate patterns existing only in the training data. However, the impressive generalization performance of over-parameterized neural networks with only implicit regularization challenges this traditional role of explicit regularization. Furthermore, explicit regularization does not prevent neural networks from memorizing unnatural patterns, such as random labels, that cannot be generalized. In this work, we revisit the role and importance of explicit regularization methods for generalizing the predictive probability, not just the generalization of the 0-1 loss. Specifically, we present extensive empirical evidence showing the versatility of explicit regularization techniques on improving the reliability of the predictive probability, which enables better uncertainty representation and prevents the overconfidence problem. Our findings present a new direction to improve the predictive probability quality of deterministic neural networks, unlike the mainstream of approaches concentrates on building stochastic representation with Bayesian neural networks, ensemble methods, and hybrid models.

Being Bayesian about Categorical Probability

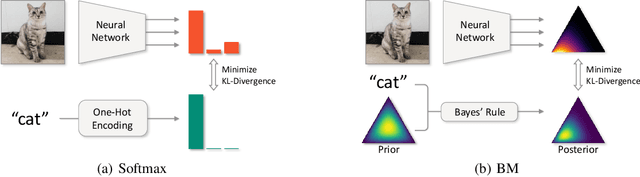
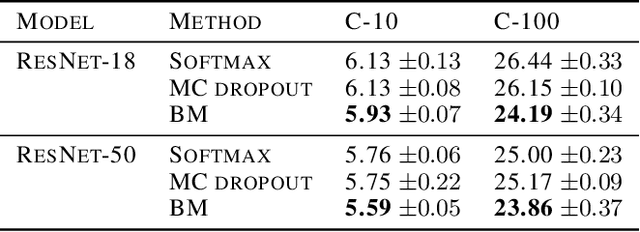
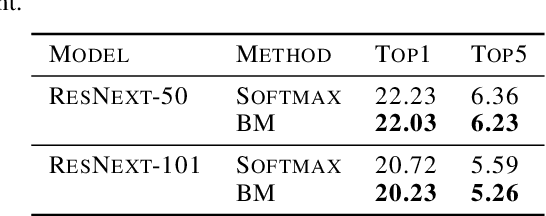
Neural networks utilize the softmax as a building block in classification tasks, which contains an overconfidence problem and lacks an uncertainty representation ability. As a Bayesian alternative to the softmax, we consider a random variable of a categorical probability over class labels. In this framework, the prior distribution explicitly models the presumed noise inherent in the observed label, which provides consistent gains in generalization performance in multiple challenging tasks. The proposed method inherits advantages of Bayesian approaches that achieve better uncertainty estimation and model calibration. Our method can be implemented as a plug-and-play loss function with negligible computational overhead compared to the softmax with the cross-entropy loss function.