Reinforcement Learning with Ensemble Model Predictive Safety Certification

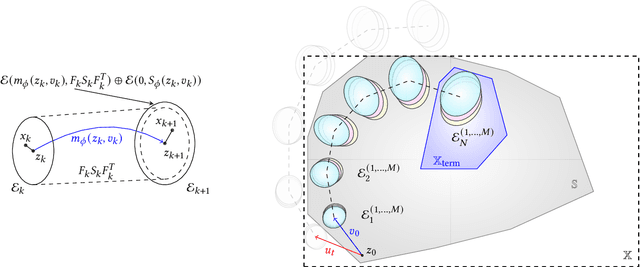
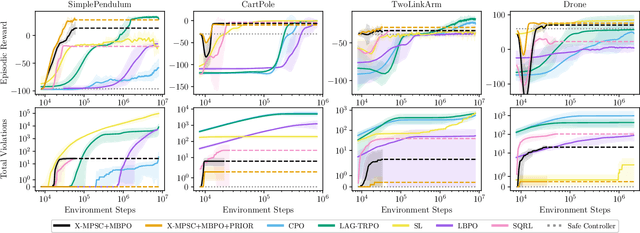
Reinforcement learning algorithms need exploration to learn. However, unsupervised exploration prevents the deployment of such algorithms on safety-critical tasks and limits real-world deployment. In this paper, we propose a new algorithm called Ensemble Model Predictive Safety Certification that combines model-based deep reinforcement learning with tube-based model predictive control to correct the actions taken by a learning agent, keeping safety constraint violations at a minimum through planning. Our approach aims to reduce the amount of prior knowledge about the actual system by requiring only offline data generated by a safe controller. Our results show that we can achieve significantly fewer constraint violations than comparable reinforcement learning methods.

Using Simulation Optimization to Improve Zero-shot Policy Transfer of Quadrotors

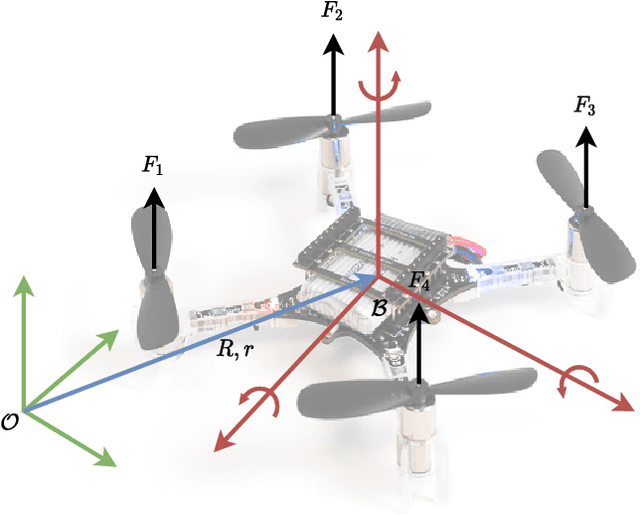
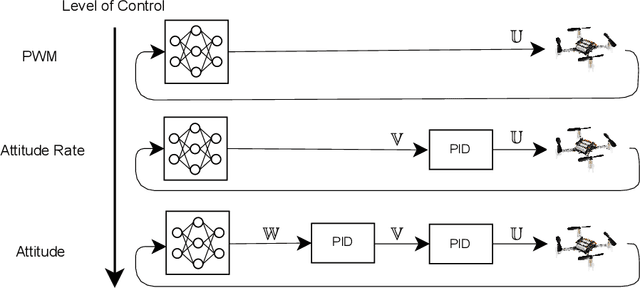
In this work, we show that it is possible to train low-level control policies with reinforcement learning entirely in simulation and, then, deploy them on a quadrotor robot without using real-world data to fine-tune. To render zero-shot policy transfers feasible, we apply simulation optimization to narrow the reality gap. Our neural network-based policies use only onboard sensor data and run entirely on the embedded drone hardware. In extensive real-world experiments, we compare three different control structures ranging from low-level pulse-width-modulated motor commands to high-level attitude control based on nested proportional-integral-derivative controllers. Our experiments show that low-level controllers trained with reinforcement learning require a more accurate simulation than higher-level control policies.

Analysis and Optimisation of Bellman Residual Errors with Neural Function Approximation

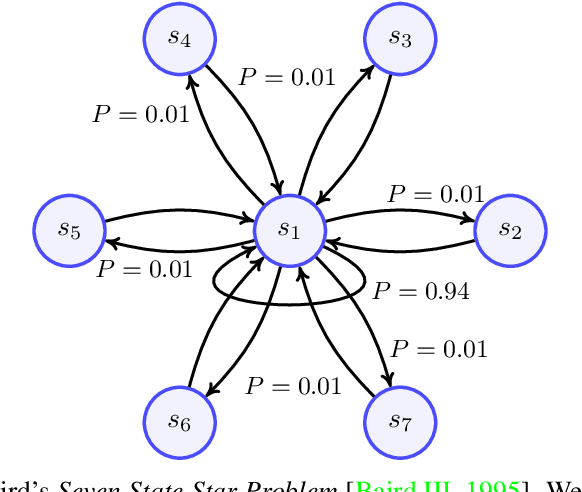
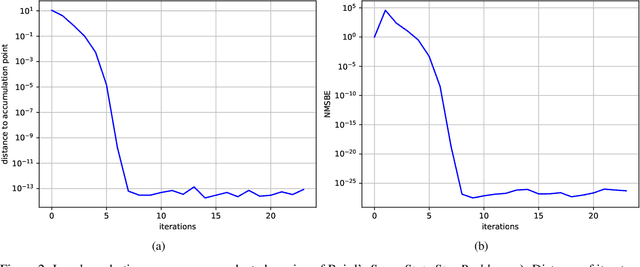
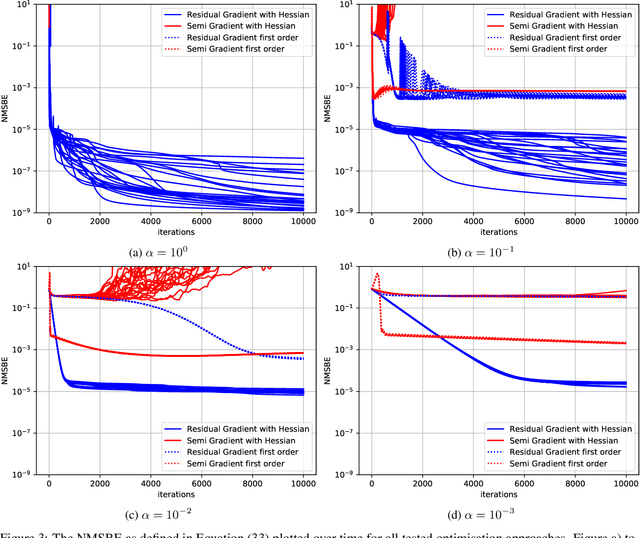
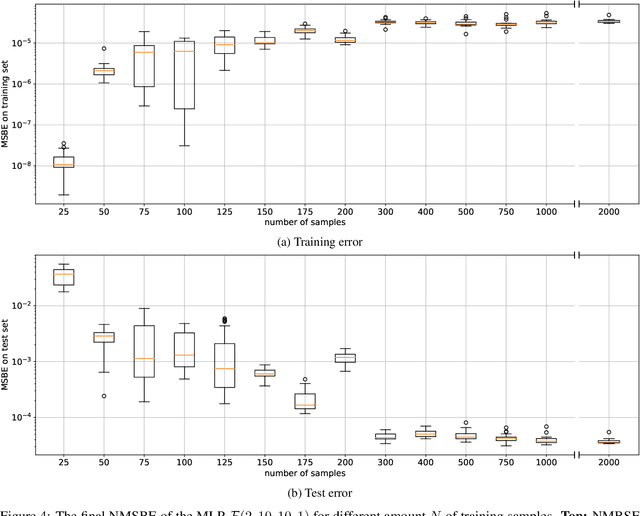
Recent development of Deep Reinforcement Learning has demonstrated superior performance of neural networks in solving challenging problems with large or even continuous state spaces. One specific approach is to deploy neural networks to approximate value functions by minimising the Mean Squared Bellman Error function. Despite great successes of Deep Reinforcement Learning, development of reliable and efficient numerical algorithms to minimise the Bellman Error is still of great scientific interest and practical demand. Such a challenge is partially due to the underlying optimisation problem being highly non-convex or using incorrect gradient information as done in Semi-Gradient algorithms. In this work, we analyse the Mean Squared Bellman Error from a smooth optimisation perspective combined with a Residual Gradient formulation. Our contribution is two-fold. First, we analyse critical points of the error function and provide technical insights on the optimisation procure and design choices for neural networks. When the existence of global minima is assumed and the objective fulfils certain conditions we can eliminate suboptimal local minima when using over-parametrised neural networks. We can construct an efficient Approximate Newton's algorithm based on our analysis and confirm theoretical properties of this algorithm such as being locally quadratically convergent to a global minimum numerically. Second, we demonstrate feasibility and generalisation capabilities of the proposed algorithm empirically using continuous control problems and provide a numerical verification of our critical point analysis. We outline the short coming of Semi-Gradients. To benefit from an approximate Newton's algorithm complete derivatives of the Mean Squared Bellman error must be considered during training.