Suresh Bhavnani
Query Learning with Exponential Query Costs
Feb 21, 2010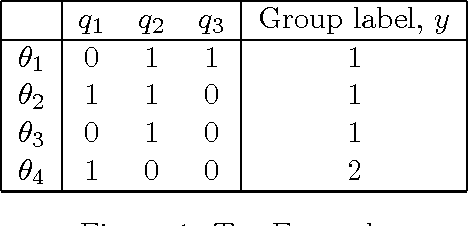
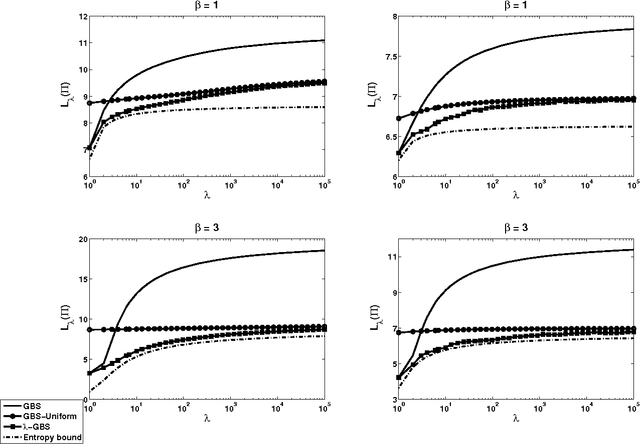
Abstract:In query learning, the goal is to identify an unknown object while minimizing the number of "yes" or "no" questions (queries) posed about that object. A well-studied algorithm for query learning is known as generalized binary search (GBS). We show that GBS is a greedy algorithm to optimize the expected number of queries needed to identify the unknown object. We also generalize GBS in two ways. First, we consider the case where the cost of querying grows exponentially in the number of queries and the goal is to minimize the expected exponential cost. Then, we consider the case where the objects are partitioned into groups, and the objective is to identify only the group to which the object belongs. We derive algorithms to address these issues in a common, information-theoretic framework. In particular, we present an exact formula for the objective function in each case involving Shannon or Renyi entropy, and develop a greedy algorithm for minimizing it. Our algorithms are demonstrated on two applications of query learning, active learning and emergency response.
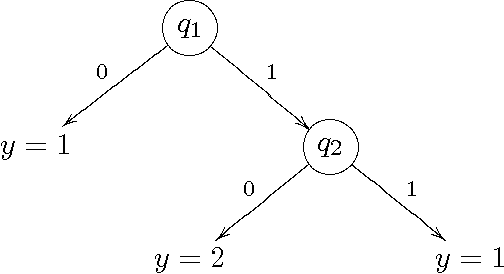
Group-based Query Learning for rapid diagnosis in time-critical situations
Nov 24, 2009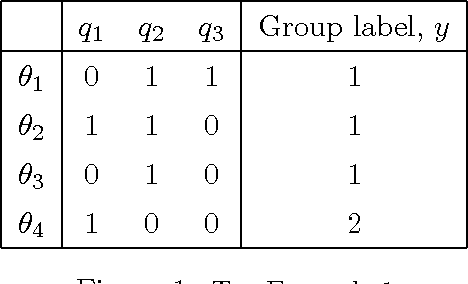



Abstract:In query learning, the goal is to identify an unknown object while minimizing the number of "yes or no" questions (queries) posed about that object. We consider three extensions of this fundamental problem that are motivated by practical considerations in real-world, time-critical identification tasks such as emergency response. First, we consider the problem where the objects are partitioned into groups, and the goal is to identify only the group to which the object belongs. Second, we address the situation where the queries are partitioned into groups, and an algorithm may suggest a group of queries to a human user, who then selects the actual query. Third, we consider the problem of query learning in the presence of persistent query noise, and relate it to group identification. To address these problems we show that a standard algorithm for query learning, known as the splitting algorithm or generalized binary search, may be viewed as a generalization of Shannon-Fano coding. We then extend this result to the group-based settings, leading to new algorithms. The performance of our algorithms is demonstrated on simulated data and on a database used by first responders for toxic chemical identification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge