Joint Approximation of Information and Distributed Link-Scheduling Decisions in Wireless Networks

For a large multi-hop wireless network, nodes are preferable to make distributed and localized link-scheduling decisions with only interactions among a small number of neighbors. However, for a slowly decaying channel and densely populated interferers, a small size neighborhood often results in nontrivial link outages and is thus insufficient for making optimal scheduling decisions. A question arises how to deal with the information outside a neighborhood in distributed link-scheduling. In this work, we develop joint approximation of information and distributed link scheduling. We first apply machine learning approaches to model distributed link-scheduling with complete information. We then characterize the information outside a neighborhood in form of residual interference as a random loss variable. The loss variable is further characterized by either a Mean Field approximation or a normal distribution based on the Lyapunov central limit theorem. The approximated information outside a neighborhood is incorporated in a factor graph. This results in joint approximation and distributed link-scheduling in an iterative fashion. Link-scheduling decisions are first made at each individual node based on the approximated loss variables. Loss variables are then updated and used for next link-scheduling decisions. The algorithm repeats between these two phases until convergence. Interactive iterations among these variables are implemented with a message-passing algorithm over a factor graph. Simulation results show that using learned information outside a neighborhood jointly with distributed link-scheduling reduces the outage probability close to zero even for a small neighborhood.

Distributed Preemption Decisions: Probabilistic Graphical Model, Algorithm and Near-Optimality

Cooperative decision making is a vision of future network management and control. Distributed connection preemption is an important example where nodes can make intelligent decisions on allocating resources and controlling traffic flows for multi-class service networks. A challenge is that nodal decisions are spatially dependent as traffic flows trespass multiple nodes in a network. Hence the performance-complexity trade-off becomes important, i.e., how accurate decisions are versus how much information is exchanged among nodes. Connection preemption is known to be NP-complete. Centralized preemption is optimal but computationally intractable. Decentralized preemption is computationally efficient but may result in a poor performance. This work investigates distributed preemption where nodes decide whether and which flows to preempt using only local information exchange with neighbors. We develop, based on the probabilistic graphical models, a near-optimal distributed algorithm. The algorithm is used by each node to make collectively near-optimal preemption decisions. We study trade-offs between near-optimal performance and complexity that corresponds to the amount of information-exchange of the distributed algorithm. The algorithm is validated by both analysis and simulation.

Randomized Distributed Configuration Management of Wireless Networks: Multi-layer Markov Random Fields and Near-Optimality

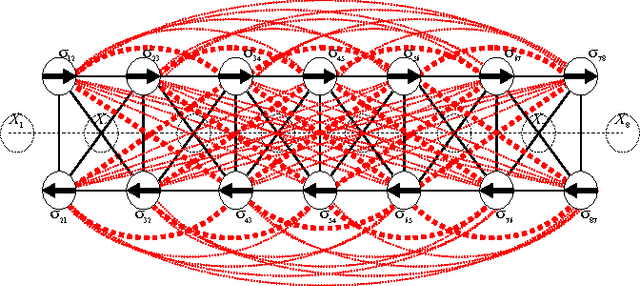
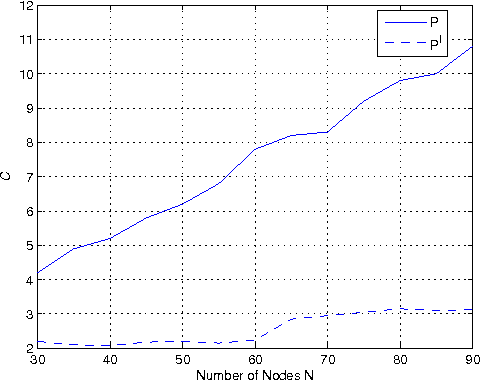
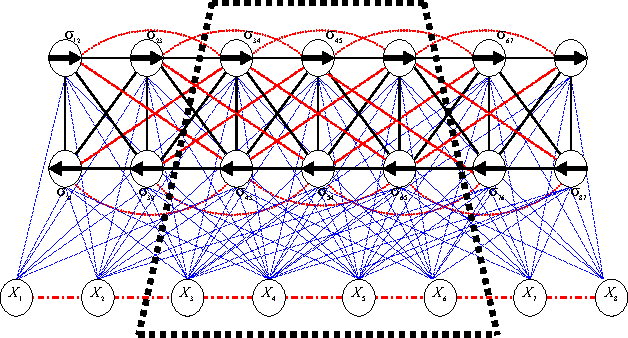
Distributed configuration management is imperative for wireless infrastructureless networks where each node adjusts locally its physical and logical configuration through information exchange with neighbors. Two issues remain open. The first is the optimality. The second is the complexity. We study these issues through modeling, analysis, and randomized distributed algorithms. Modeling defines the optimality. We first derive a global probabilistic model for a network configuration which characterizes jointly the statistical spatial dependence of a physical- and a logical-configuration. We then show that a local model which approximates the global model is a two-layer Markov Random Field or a random bond model. The complexity of the local model is the communication range among nodes. The local model is near-optimal when the approximation error to the global model is within a given error bound. We analyze the trade-off between an approximation error and complexity, and derive sufficient conditions on the near-optimality of the local model. We validate the model, the analysis and the randomized distributed algorithms also through simulation.