Randomized Distributed Configuration Management of Wireless Networks: Multi-layer Markov Random Fields and Near-Optimality

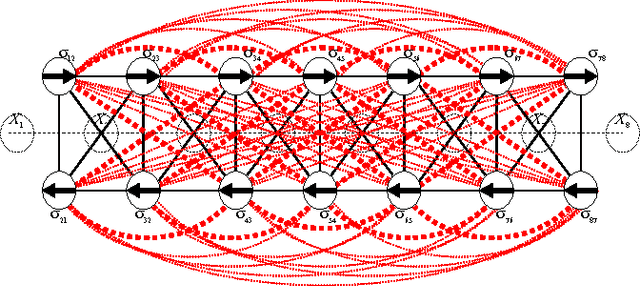
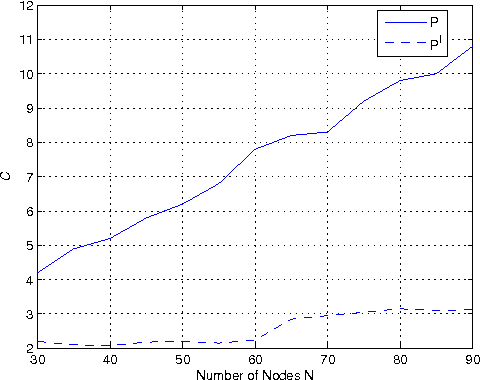
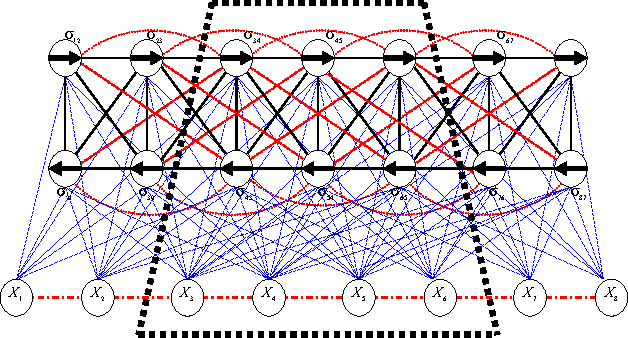
Distributed configuration management is imperative for wireless infrastructureless networks where each node adjusts locally its physical and logical configuration through information exchange with neighbors. Two issues remain open. The first is the optimality. The second is the complexity. We study these issues through modeling, analysis, and randomized distributed algorithms. Modeling defines the optimality. We first derive a global probabilistic model for a network configuration which characterizes jointly the statistical spatial dependence of a physical- and a logical-configuration. We then show that a local model which approximates the global model is a two-layer Markov Random Field or a random bond model. The complexity of the local model is the communication range among nodes. The local model is near-optimal when the approximation error to the global model is within a given error bound. We analyze the trade-off between an approximation error and complexity, and derive sufficient conditions on the near-optimality of the local model. We validate the model, the analysis and the randomized distributed algorithms also through simulation.