Sung-Hsien Hsieh
Fast Binary Embedding via Circulant Downsampled Matrix -- A Data-Independent Approach
Jan 24, 2016



Abstract:Binary embedding of high-dimensional data aims to produce low-dimensional binary codes while preserving discriminative power. State-of-the-art methods often suffer from high computation and storage costs. We present a simple and fast embedding scheme by first downsampling N-dimensional data into M-dimensional data and then multiplying the data with an MxM circulant matrix. Our method requires O(N +M log M) computation and O(N) storage costs. We prove if data have sparsity, our scheme can achieve similarity-preserving well. Experiments further demonstrate that though our method is cost-effective and fast, it still achieves comparable performance in image applications.
Fast Template Matching by Subsampled Circulant Matrix
Sep 16, 2015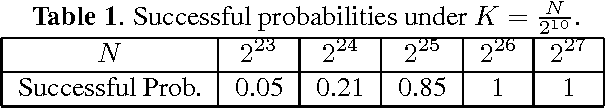
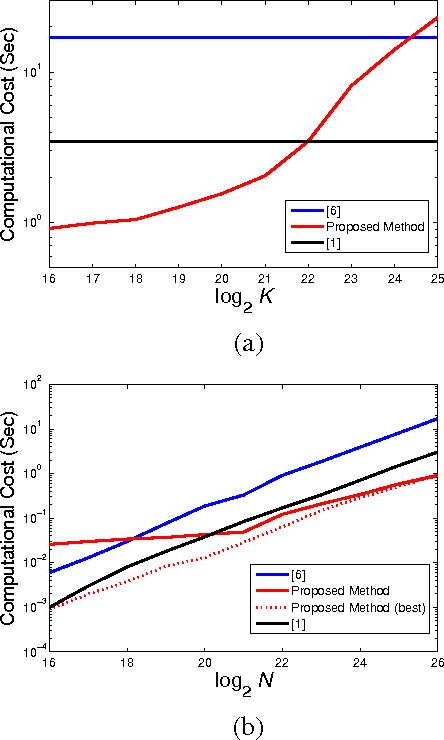
Abstract:Template matching is widely used for many applications in image and signal processing and usually is time-critical. Traditional methods usually focus on how to reduce the search locations by coarse-to-fine strategy or full search combined with pruning strategy. However, the computation cost of those methods is easily dominated by the size of signal N instead of that of template K. This paper proposes a probabilistic and fast matching scheme, which computation costs requires O(N) additions and O(K \log K) multiplications, based on cross-correlation. The nuclear idea is to first downsample signal, which size becomes O(K), and then subsequent operations only involves downsampled signals. The probability of successful match depends on cross-correlation between signal and the template. We show the sufficient condition for successful match and prove that the probability is high for binary signals with K^2/log K >= O(N). The experiments shows this proposed scheme is fast and efficient and supports the theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge