Approximation Algorithms for Bayesian Multi-Armed Bandit Problems

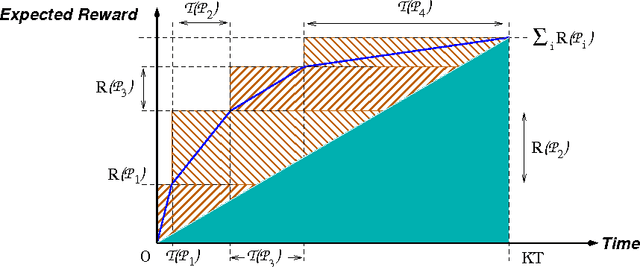
In this paper, we consider several finite-horizon Bayesian multi-armed bandit problems with side constraints which are computationally intractable (NP-Hard) and for which no optimal (or near optimal) algorithms are known to exist with sub-exponential running time. All of these problems violate the standard exchange property, which assumes that the reward from the play of an arm is not contingent upon when the arm is played. Not only are index policies suboptimal in these contexts, there has been little analysis of such policies in these problem settings. We show that if we consider near-optimal policies, in the sense of approximation algorithms, then there exists (near) index policies. Conceptually, if we can find policies that satisfy an approximate version of the exchange property, namely, that the reward from the play of an arm depends on when the arm is played to within a constant factor, then we have an avenue towards solving these problems. However such an approximate version of the idling bandit property does not hold on a per-play basis and are shown to hold in a global sense. Clearly, such a property is not necessarily true of arbitrary single arm policies and finding such single arm policies is nontrivial. We show that by restricting the state spaces of arms we can find single arm policies and that these single arm policies can be combined into global (near) index policies where the approximate version of the exchange property is true in expectation. The number of different bandit problems that can be addressed by this technique already demonstrate its wide applicability.

Multiarmed Bandit Problems with Delayed Feedback

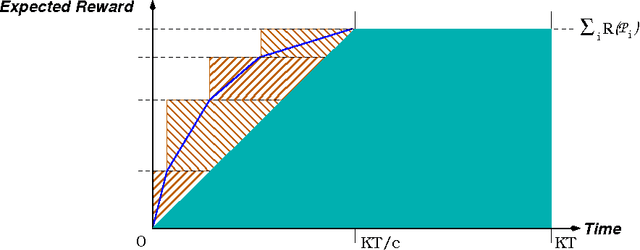
In this paper we initiate the study of optimization of bandit type problems in scenarios where the feedback of a play is not immediately known. This arises naturally in allocation problems which have been studied extensively in the literature, albeit in the absence of delays in the feedback. We study this problem in the Bayesian setting. In presence of delays, no solution with provable guarantees is known to exist with sub-exponential running time. We show that bandit problems with delayed feedback that arise in allocation settings can be forced to have significant structure, with a slight loss in optimality. This structure gives us the ability to reason about the relationship of single arm policies to the entangled optimum policy, and eventually leads to a O(1) approximation for a significantly general class of priors. The structural insights we develop are of key interest and carry over to the setting where the feedback of an action is available instantaneously, and we improve all previous results in this setting as well.