A Generalized Mean Approach for Distributed-PCA

Principal component analysis (PCA) is a widely used technique for dimension reduction. As datasets continue to grow in size, distributed-PCA (DPCA) has become an active research area. A key challenge in DPCA lies in efficiently aggregating results across multiple machines or computing nodes due to computational overhead. Fan et al. (2019) introduced a pioneering DPCA method to estimate the leading rank-$r$ eigenspace, aggregating local rank-$r$ projection matrices by averaging. However, their method does not utilize eigenvalue information. In this article, we propose a novel DPCA method that incorporates eigenvalue information to aggregate local results via the matrix $\beta$-mean, which we call $\beta$-DPCA. The matrix $\beta$-mean offers a flexible and robust aggregation method through the adjustable choice of $\beta$ values. Notably, for $\beta=1$, it corresponds to the arithmetic mean; for $\beta=-1$, the harmonic mean; and as $\beta \to 0$, the geometric mean. Moreover, the matrix $\beta$-mean is shown to associate with the matrix $\beta$-divergence, a subclass of the Bregman matrix divergence, to support the robustness of $\beta$-DPCA. We also study the stability of eigenvector ordering under eigenvalue perturbation for $\beta$-DPCA. The performance of our proposal is evaluated through numerical studies.

TensorProjection Layer: A Tensor-Based Dimensionality Reduction Method in CNN

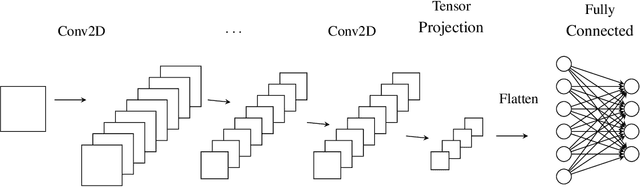
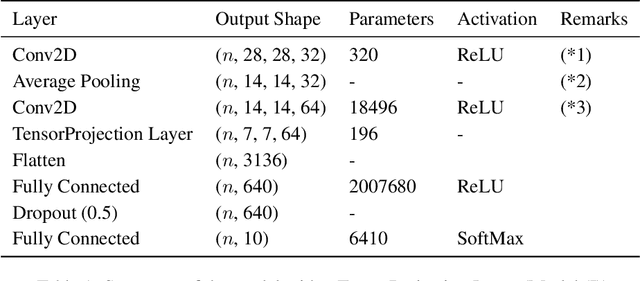
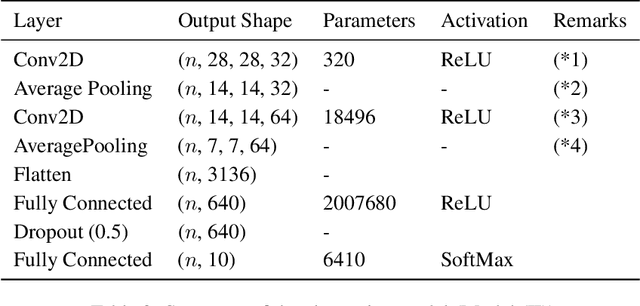
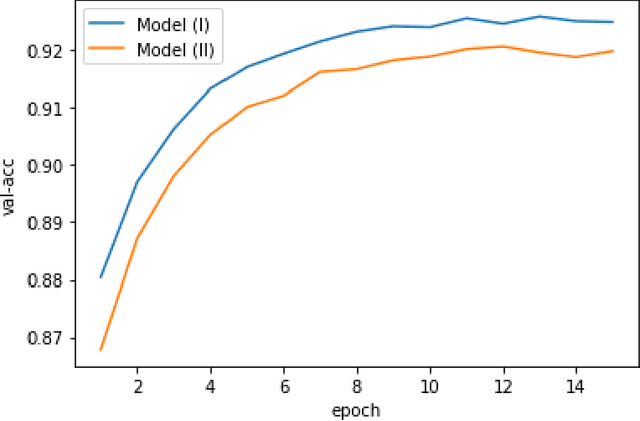
In this paper, we propose a dimensionality reduction method applied to tensor-structured data as a hidden layer (we call it TensorProjection Layer) in a convolutional neural network. Our proposed method transforms input tensors into ones with a smaller dimension by projection. The directions of projection are viewed as training parameters associated with our proposed layer and trained via a supervised learning criterion such as minimization of the cross-entropy loss function. We discuss the gradients of the loss function with respect to the parameters associated with our proposed layer. We also implement simple numerical experiments to evaluate the performance of the TensorProjection Layer.

2SDR: Applying Kronecker Envelope PCA to denoise Cryo-EM Images

Principal component analysis (PCA) is arguably the most widely used dimension reduction method for vector type data. When applied to image data, PCA demands the images to be portrayed as vectors. The resulting computation is heavy because it will solve an eigenvalue problem of a huge covariance matrix due to the vectorization step. To mitigate the computation burden, multilinear PCA (MPCA) that generates each basis vector using a column vector and a row vector with a Kronecker product was introduced, for which the success was demonstrated on face image sets. However, when we apply MPCA on the cryo-electron microscopy (cryo-EM) particle images, the results are not satisfactory when compared with PCA. On the other hand, to compare the reduced spaces as well as the number of parameters of MPCA and PCA, Kronecker Envelope PCA (KEPCA) was proposed to provide a PCA-like basis from MPCA. Here, we apply KEPCA to denoise cryo-EM images through a two-stage dimension reduction (2SDR) algorithm. 2SDR first applies MPCA to extract the projection scores and then applies PCA on these scores to further reduce the dimension. 2SDR has two benefits that it inherits the computation advantage of MPCA and its projection scores are uncorrelated as those of PCA. Testing with three cryo-EM benchmark experimental datasets shows that 2SDR performs better than MPCA and PCA alone in terms of the computation efficiency and denoising quality. Remarkably, the denoised particles boxed out from the 2SDR-denoised micrographs allow subsequent structural analysis to reach a high-quality 3D density map. This demonstrates that the high resolution information can be well preserved through this 2SDR denoising strategy.

Functional Inverse Regression in an Enlarged Dimension Reduction Space

We consider an enlarged dimension reduction space in functional inverse regression. Our operator and functional analysis based approach facilitates a compact and rigorous formulation of the functional inverse regression problem. It also enables us to expand the possible space where the dimension reduction functions belong. Our formulation provides a unified framework so that the classical notions, such as covariance standardization, Mahalanobis distance, SIR and linear discriminant analysis, can be naturally and smoothly carried out in our enlarged space. This enlarged dimension reduction space also links to the linear discriminant space of Gaussian measures on a separable Hilbert space.