Steven A. Gabriel
Using Inverse Optimization to Learn Cost Functions in Generalized Nash Games
Feb 24, 2021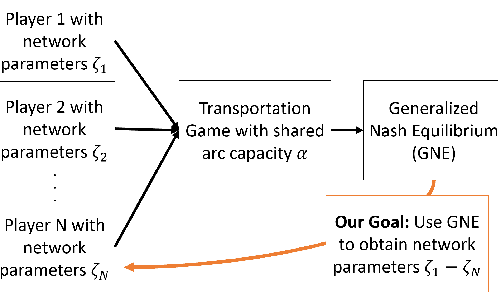
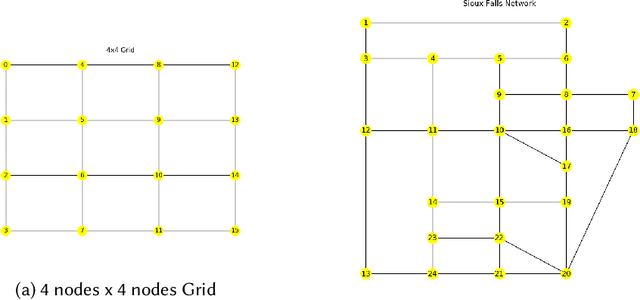
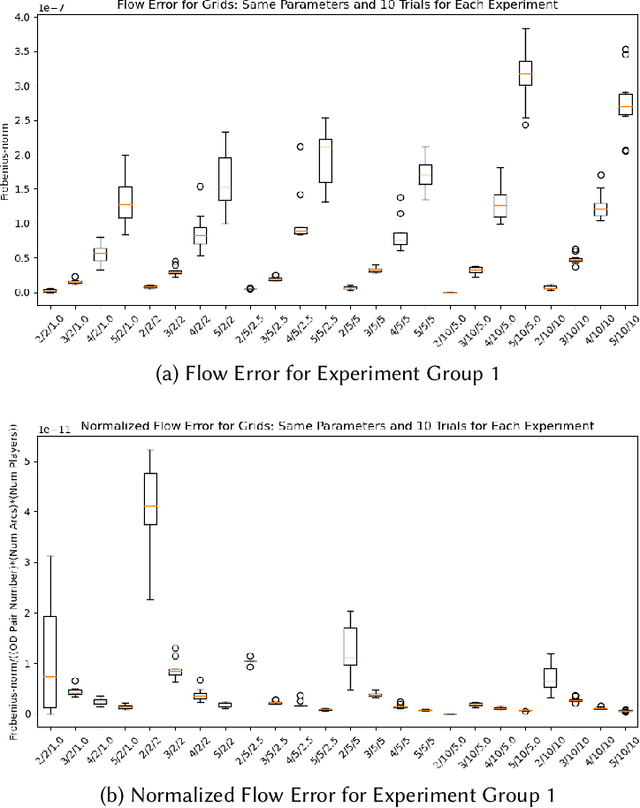
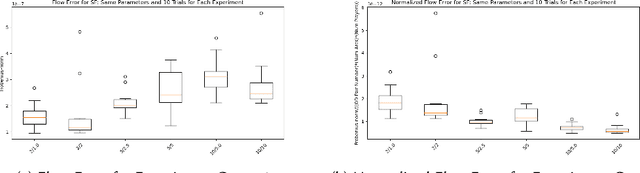
Abstract:As demonstrated by Ratliff et al. (2014), inverse optimization can be used to recover the objective function parameters of players in multi-player Nash games. These games involve the optimization problems of multiple players in which the players can affect each other in their objective functions. In generalized Nash equilibrium problems (GNEPs), a player's set of feasible actions is also impacted by the actions taken by other players in the game; see Facchinei and Kanzow (2010) for more background on this problem. One example of such impact comes in the form of joint/"coupled" constraints as referenced by Rosen (1965), Harker (1991), and Facchinei et al. (2007) which involve other players' variables in the constraints of the feasible region. We extend the framework of Ratliff et al. (2014) to find inverse optimization solutions for the class of GNEPs with joint constraints. The resulting formulation is then applied to a simulated multi-player transportation problem on a road network. Also, we provide some theoretical results related to this transportation problem regarding runtime of the extended framework as well as uniqueness and non-uniqueness of solutions to our simulation experiments. We see that our model recovers parameterizations that produce the same flow patterns as the original parameterizations and that this holds true across multiple networks, different assumptions regarding players' perceived costs, and the majority of restrictive capacity settings and the associated numbers of players. Code for the project can be found at: https://github.com/sallen7/IO_GNEP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge