Stephen Marsland
Classifying Organisms and Artefacts By Their Shapes
Aug 27, 2021

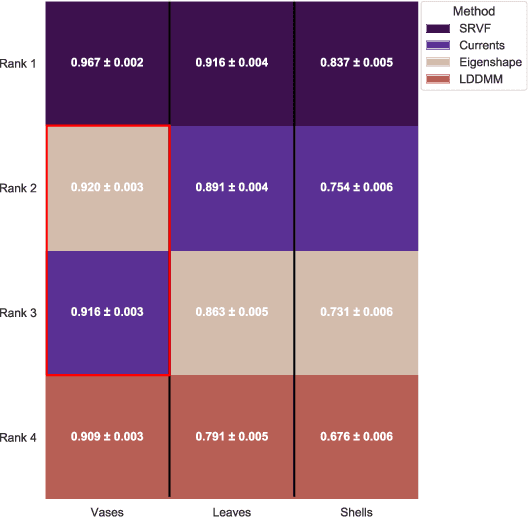

Abstract:We often wish to classify objects by their shapes. Indeed, the study of shapes is an important part of many scientific fields such as evolutionary biology, structural biology, image processing, and archaeology. The most widely-used method of shape analysis, Geometric Morphometrics, assumes that that the mathematical space in which shapes are represented is linear. However, it has long been known that shape space is, in fact, rather more complicated, and certainly non-linear. Diffeomorphic methods that take this non-linearity into account, and so give more accurate estimates of the distances among shapes, exist but have rarely been applied to real-world problems. Using a machine classifier, we tested the ability of several of these methods to describe and classify the shapes of a variety of organic and man-made objects. We find that one method, the Square-Root Velocity Function (SRVF), is superior to all others, including a standard Geometric Morphometric method (eigenshapes). We also show that computational shape classifiers outperform human experts, and that the SRVF shortest-path between shapes can be used to estimate the shapes of intermediate steps in evolutionary series. Diffeomorphic shape analysis methods, we conclude, now provide practical and effective solutions to many shape description and classification problems in the natural and human sciences.
Möbius Invariants of Shapes and Images
Aug 11, 2016



Abstract:Identifying when different images are of the same object despite changes caused by imaging technologies, or processes such as growth, has many applications in fields such as computer vision and biological image analysis. One approach to this problem is to identify the group of possible transformations of the object and to find invariants to the action of that group, meaning that the object has the same values of the invariants despite the action of the group. In this paper we study the invariants of planar shapes and images under the M\"obius group $\mathrm{PSL}(2,\mathbb{C})$, which arises in the conformal camera model of vision and may also correspond to neurological aspects of vision, such as grouping of lines and circles. We survey properties of invariants that are important in applications, and the known M\"obius invariants, and then develop an algorithm by which shapes can be recognised that is M\"obius- and reparametrization-invariant, numerically stable, and robust to noise. We demonstrate the efficacy of this new invariant approach on sets of curves, and then develop a M\"obius-invariant signature of grey-scale images.
K-Bit-Swap: A New Operator For Real-Coded Evolutionary Algorithms
Apr 22, 2016


Abstract:There has been a variety of crossover operators proposed for Real-Coded Genetic Algorithms (RCGAs), which recombine values from the same location in pairs of strings. In this article we present a recombination operator for RC- GAs that selects the locations randomly in both parents, and compare it to mainstream crossover operators in a set of experiments on a range of standard multidimensional optimization problems and a clustering problem. We present two variants of the operator, either selecting both bits uniformly at random in the strings, or sampling the second bit from a normal distribution centered at the selected location in the first string. While the operator is biased towards exploitation of fitness space, the random selection of the second bit for swap- ping makes it slightly less exploitation-biased. Extensive statistical analysis using a non-parametric test shows the advantage of the new recombination operators on a range of test functions.
Principal Autoparallel Analysis: Data Analysis in Weitzenböck Space
Nov 11, 2015



Abstract:The statistical analysis of data lying on a differentiable, locally Euclidean, manifold introduces a variety of challenges because the analogous measures to standard Euclidean statistics are local, that is only defined within a neighbourhood of each datapoint. This is because the curvature of the space means that the connection of Riemannian geometry is path dependent. In this paper we transfer the problem to Weitzenb\"{o}ck space, which has torsion, but not curvature, meaning that parallel transport is path independent, and rather than considering geodesics, it is natural to consider autoparallels, which are `straight' in the sense that they follow the local basis vectors. We demonstrate how to generate these autoparallels in a data-driven fashion, and show that the resulting representation of the data is a useful space in which to perform further analysis.
Derivation of Upper Bounds on Optimization Time of Population-Based Evolutionary Algorithm on a Function with Fitness Plateaus Using Elitism Levels Traverse Mechanism
Aug 30, 2013
Abstract:In this article a tool for the analysis of population-based EAs is used to derive asymptotic upper bounds on the optimization time of the algorithm solving Royal Roads problem, a test function with plateaus of fitness. In addition to this, limiting distribution of a certain subset of the population is approximated.
Convergence of a Recombination-Based Elitist Evolutionary Algorithm on the Royal Roads Test Function
Aug 24, 2011

Abstract:We present an analysis of the performance of an elitist Evolutionary algorithm using a recombination operator known as 1-Bit-Swap on the Royal Roads test function based on a population. We derive complete, approximate and asymptotic convergence rates for the algorithm. The complete model shows the benefit of the size of the population and re- combination pool.
Convergence Properties of Two (μ + λ) Evolutionary Algorithms On OneMax and Royal Roads Test Functions
Aug 20, 2011



Abstract:We present a number of bounds on convergence time for two elitist population-based Evolutionary Algorithms using a recombination operator k-Bit-Swap and a mainstream Randomized Local Search algorithm. We study the effect of distribution of elite species and population size.
Novelty Detection on a Mobile Robot Using Habituation
Jun 02, 2000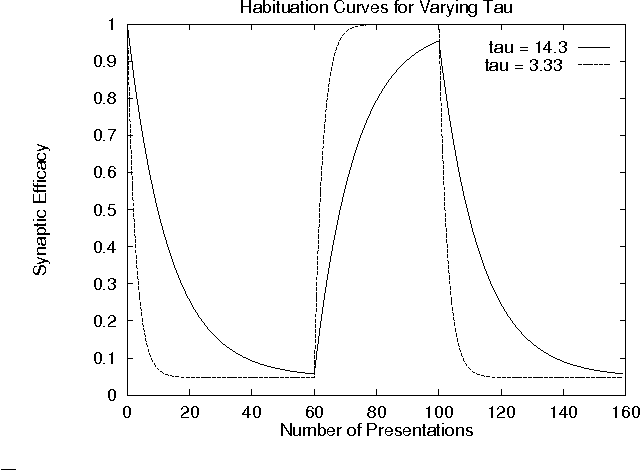
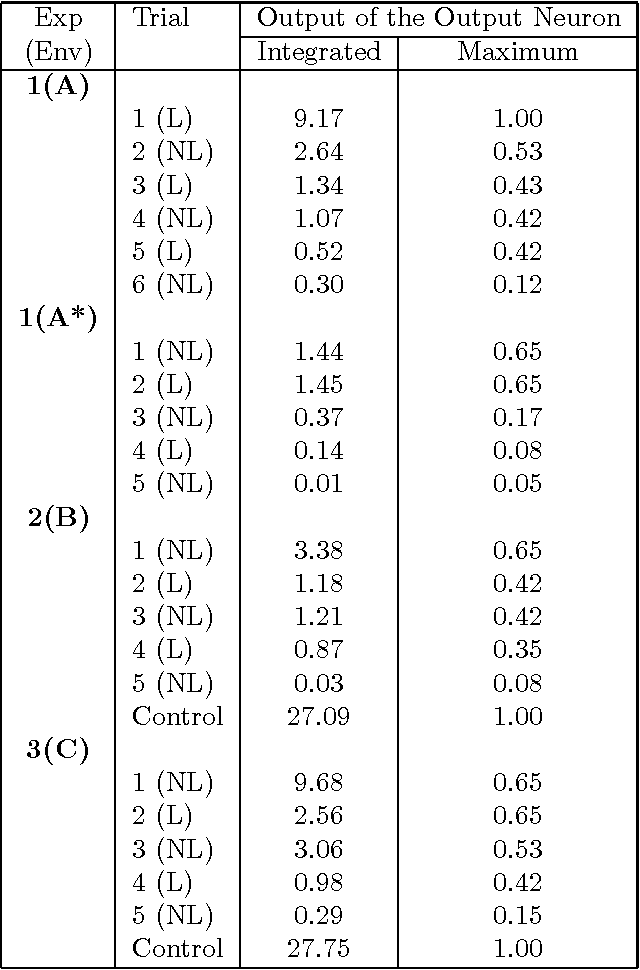
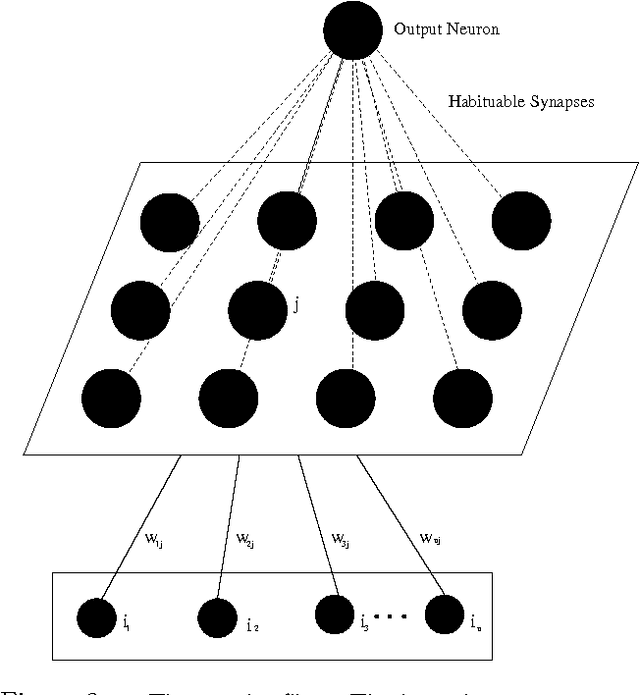
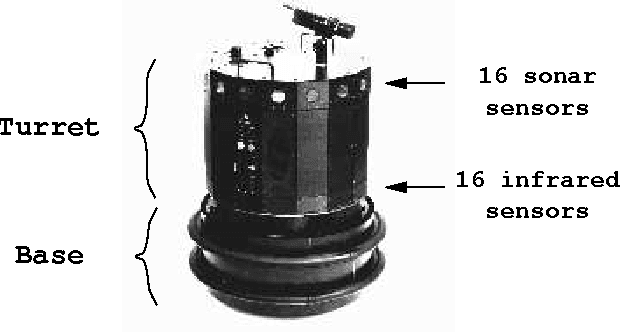
Abstract:In this paper a novelty filter is introduced which allows a robot operating in an un structured environment to produce a self-organised model of its surroundings and to detect deviations from the learned model. The environment is perceived using the rob ot's 16 sonar sensors. The algorithm produces a novelty measure for each sensor scan relative to the model it has learned. This means that it highlights stimuli which h ave not been previously experienced. The novelty filter proposed uses a model of hab ituation. Habituation is a decrement in behavioural response when a stimulus is pre sented repeatedly. Robot experiments are presented which demonstrate the reliable o peration of the filter in a number of environments.
A Real-Time Novelty Detector for a Mobile Robot
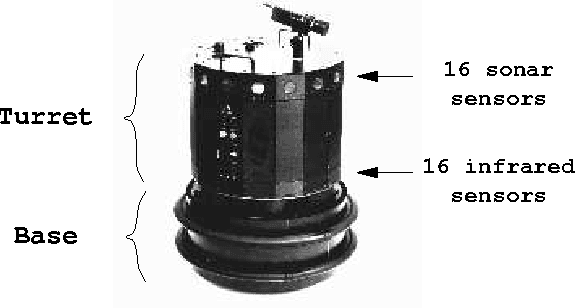
Jun 02, 2000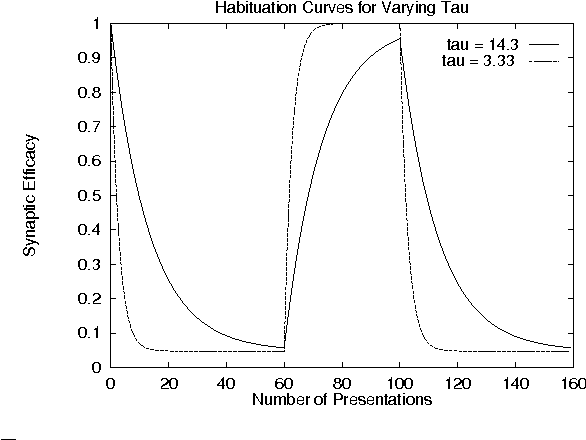
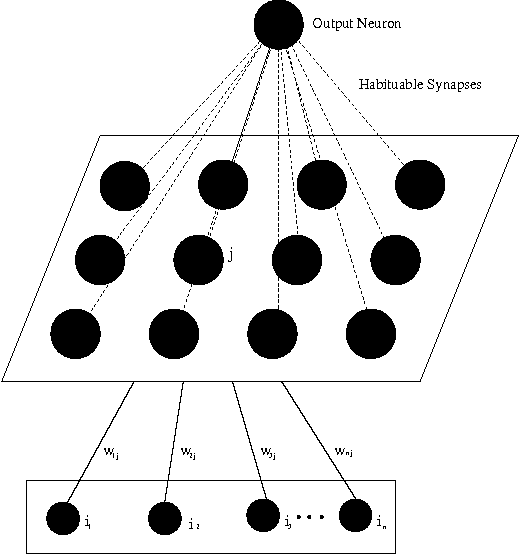
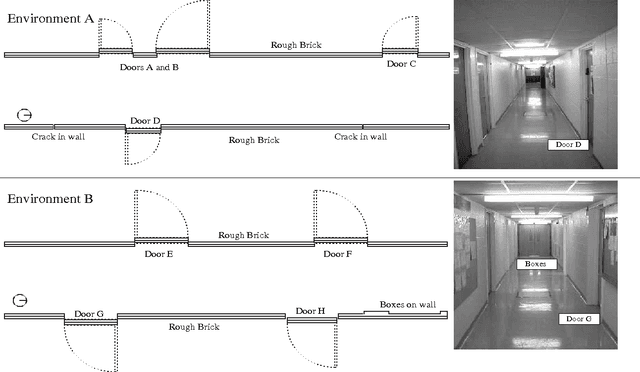
Abstract:Recognising new or unusual features of an environment is an ability which is potentially very useful to a robot. This paper demonstrates an algorithm which achieves this task by learning an internal representation of `normality' from sonar scans taken as a robot explores the environment. This model of the environment is used to evaluate the novelty of each sonar scan presented to it with relation to the model. Stimuli which have not been seen before, and therefore have more novelty, are highlighted by the filter. The filter has the ability to forget about features which have been learned, so that stimuli which are seen only rarely recover their response over time. A number of robot experiments are presented which demonstrate the operation of the filter.
Novelty Detection for Robot Neotaxis
Jun 02, 2000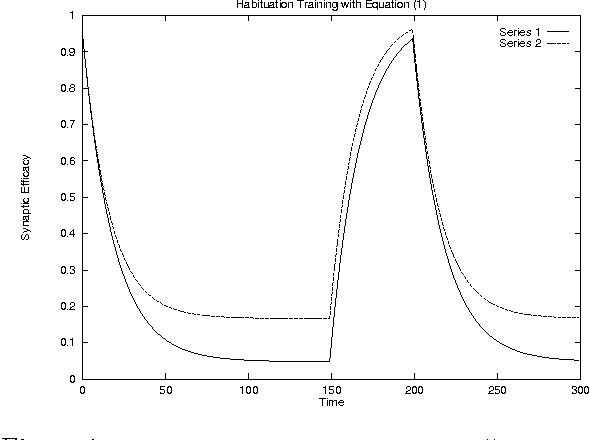
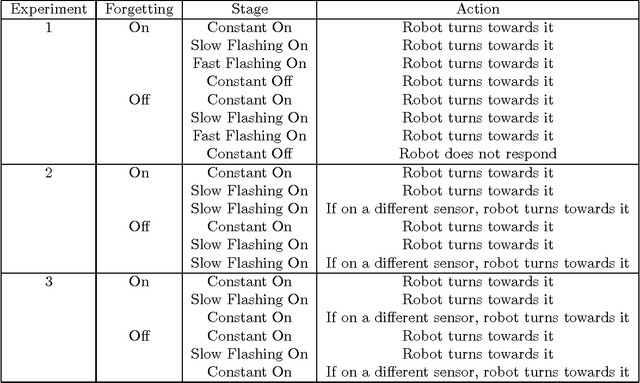
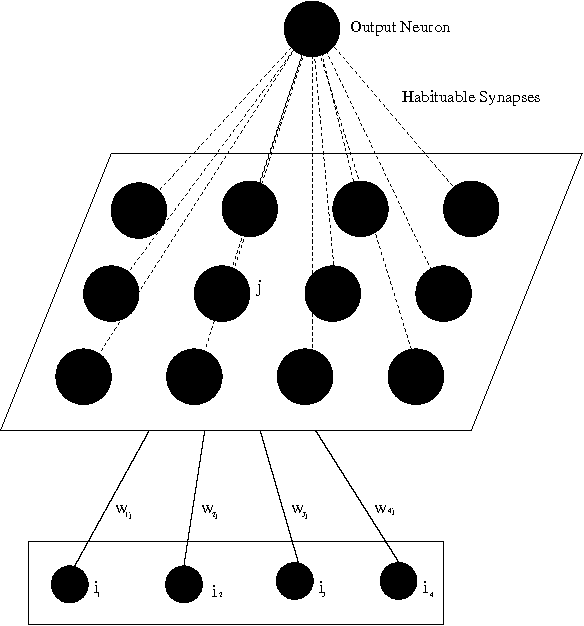

Abstract:The ability of a robot to detect and respond to changes in its environment is potentially very useful, as it draws attention to new and potentially important features. We describe an algorithm for learning to filter out previously experienced stimuli to allow further concentration on novel features. The algorithm uses a model of habituation, a biological process which causes a decrement in response with repeated presentation. Experiments with a mobile robot are presented in which the robot detects the most novel stimulus and turns towards it (`neotaxis').
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge