Classifying Organisms and Artefacts By Their Shapes
Paper and Code
Aug 27, 2021

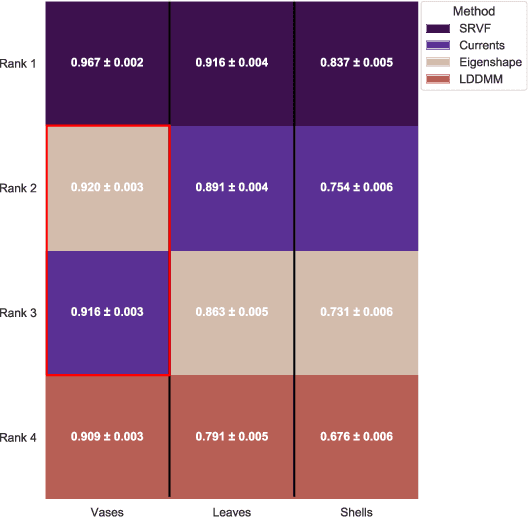

We often wish to classify objects by their shapes. Indeed, the study of shapes is an important part of many scientific fields such as evolutionary biology, structural biology, image processing, and archaeology. The most widely-used method of shape analysis, Geometric Morphometrics, assumes that that the mathematical space in which shapes are represented is linear. However, it has long been known that shape space is, in fact, rather more complicated, and certainly non-linear. Diffeomorphic methods that take this non-linearity into account, and so give more accurate estimates of the distances among shapes, exist but have rarely been applied to real-world problems. Using a machine classifier, we tested the ability of several of these methods to describe and classify the shapes of a variety of organic and man-made objects. We find that one method, the Square-Root Velocity Function (SRVF), is superior to all others, including a standard Geometric Morphometric method (eigenshapes). We also show that computational shape classifiers outperform human experts, and that the SRVF shortest-path between shapes can be used to estimate the shapes of intermediate steps in evolutionary series. Diffeomorphic shape analysis methods, we conclude, now provide practical and effective solutions to many shape description and classification problems in the natural and human sciences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge