Multi-agent Inverse Reinforcement Learning for General-sum Stochastic Games

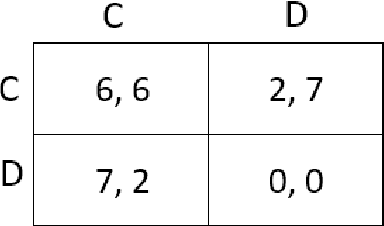
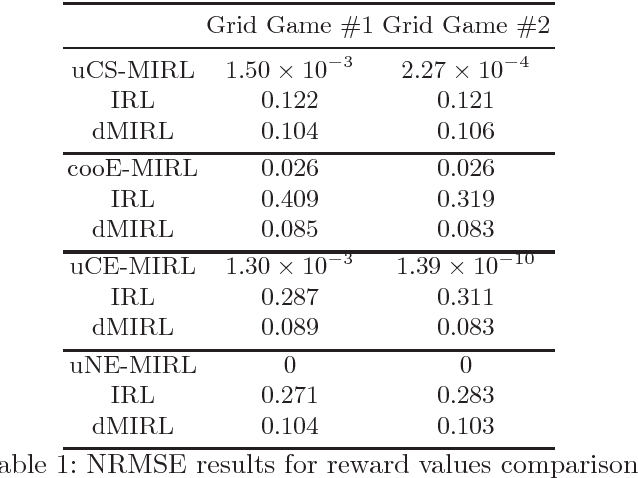
This paper addresses the problem of multi-agent inverse reinforcement learning (MIRL) in a two-player general-sum stochastic game framework. Five variants of MIRL are considered: uCS-MIRL, advE-MIRL, cooE-MIRL, uCE-MIRL, and uNE-MIRL, each distinguished by its solution concept. Problem uCS-MIRL is a cooperative game in which the agents employ cooperative strategies that aim to maximize the total game value. In problem uCE-MIRL, agents are assumed to follow strategies that constitute a correlated equilibrium while maximizing total game value. Problem uNE-MIRL is similar to uCE-MIRL in total game value maximization, but it is assumed that the agents are playing a Nash equilibrium. Problems advE-MIRL and cooE-MIRL assume agents are playing an adversarial equilibrium and a coordination equilibrium, respectively. We propose novel approaches to address these five problems under the assumption that the game observer either knows or is able to accurate estimate the policies and solution concepts for players. For uCS-MIRL, we first develop a characteristic set of solutions ensuring that the observed bi-policy is a uCS and then apply a Bayesian inverse learning method. For uCE-MIRL, we develop a linear programming problem subject to constraints that define necessary and sufficient conditions for the observed policies to be correlated equilibria. The objective is to choose a solution that not only minimizes the total game value difference between the observed bi-policy and a local uCS, but also maximizes the scale of the solution. We apply a similar treatment to the problem of uNE-MIRL. The remaining two problems can be solved efficiently by taking advantage of solution uniqueness and setting up a convex optimization problem. Results are validated on various benchmark grid-world games.