Stephane Gaiffas
Sparse Bayesian Unsupervised Learning
Jan 30, 2014



Abstract:This paper is about variable selection, clustering and estimation in an unsupervised high-dimensional setting. Our approach is based on fitting constrained Gaussian mixture models, where we learn the number of clusters $K$ and the set of relevant variables $S$ using a generalized Bayesian posterior with a sparsity inducing prior. We prove a sparsity oracle inequality which shows that this procedure selects the optimal parameters $K$ and $S$. This procedure is implemented using a Metropolis-Hastings algorithm, based on a clustering-oriented greedy proposal, which makes the convergence to the posterior very fast.
Link Prediction in Graphs with Autoregressive Features
Sep 14, 2012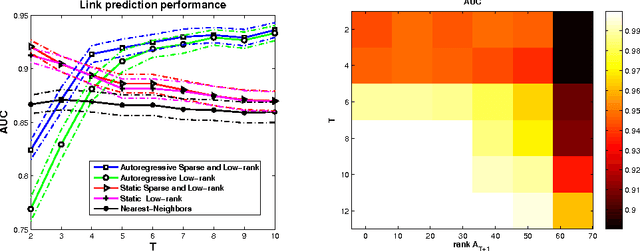
Abstract:In the paper, we consider the problem of link prediction in time-evolving graphs. We assume that certain graph features, such as the node degree, follow a vector autoregressive (VAR) model and we propose to use this information to improve the accuracy of prediction. Our strategy involves a joint optimization procedure over the space of adjacency matrices and VAR matrices which takes into account both sparsity and low rank properties of the matrices. Oracle inequalities are derived and illustrate the trade-offs in the choice of smoothing parameters when modeling the joint effect of sparsity and low rank property. The estimate is computed efficiently using proximal methods through a generalized forward-backward agorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge