On the Ability of Deep Networks to Learn Symmetries from Data: A Neural Kernel Theory

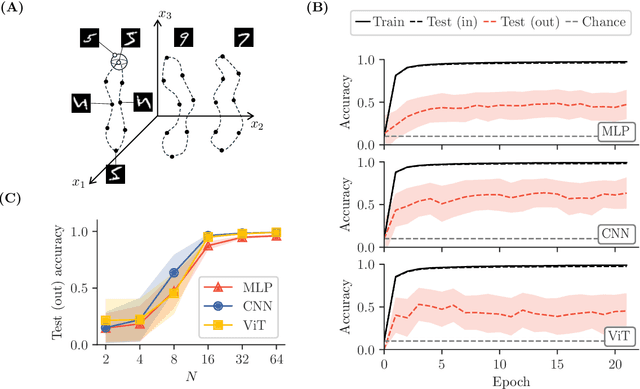
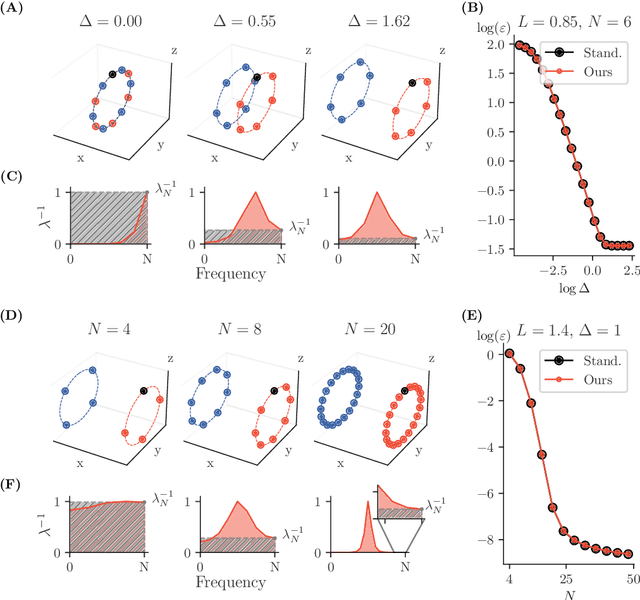
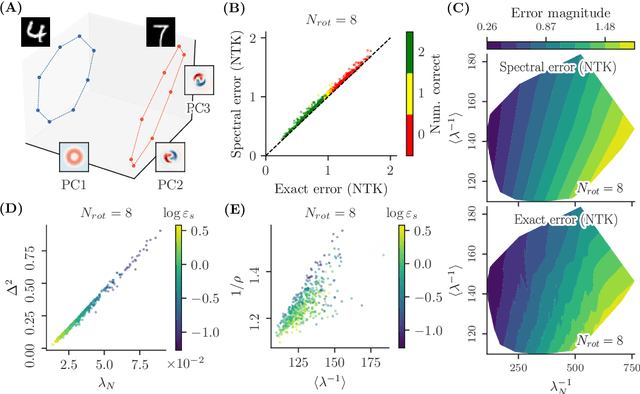
Symmetries (transformations by group actions) are present in many datasets, and leveraging them holds significant promise for improving predictions in machine learning. In this work, we aim to understand when and how deep networks can learn symmetries from data. We focus on a supervised classification paradigm where data symmetries are only partially observed during training: some classes include all transformations of a cyclic group, while others include only a subset. We ask: can deep networks generalize symmetry invariance to the partially sampled classes? In the infinite-width limit, where kernel analogies apply, we derive a neural kernel theory of symmetry learning to address this question. The group-cyclic nature of the dataset allows us to analyze the spectrum of neural kernels in the Fourier domain; here we find a simple characterization of the generalization error as a function of the interaction between class separation (signal) and class-orbit density (noise). We observe that generalization can only be successful when the local structure of the data prevails over its non-local, symmetric, structure, in the kernel space defined by the architecture. This occurs when (1) classes are sufficiently distinct and (2) class orbits are sufficiently dense. Our framework also applies to equivariant architectures (e.g., CNNs), and recovers their success in the special case where the architecture matches the inherent symmetry of the data. Empirically, our theory reproduces the generalization failure of finite-width networks (MLP, CNN, ViT) trained on partially observed versions of rotated-MNIST. We conclude that conventional networks trained with supervision lack a mechanism to learn symmetries that have not been explicitly embedded in their architecture a priori. Our framework could be extended to guide the design of architectures and training procedures able to learn symmetries from data.

A Unified Theory of Early Visual Representations from Retina to Cortex through Anatomically Constrained Deep CNNs

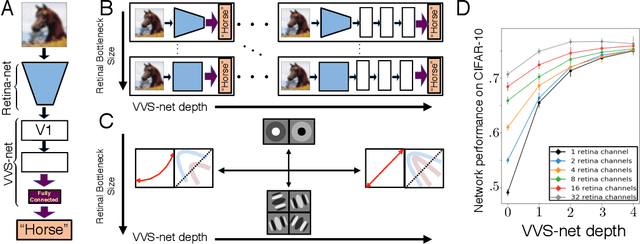
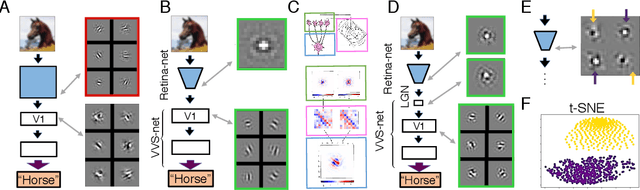
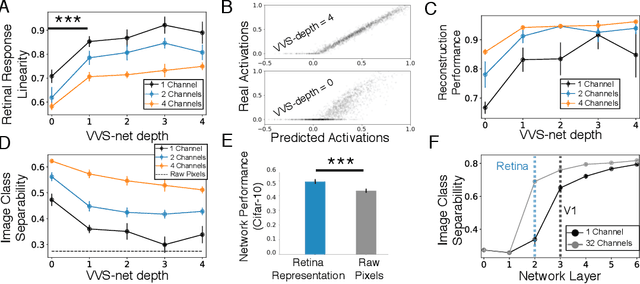
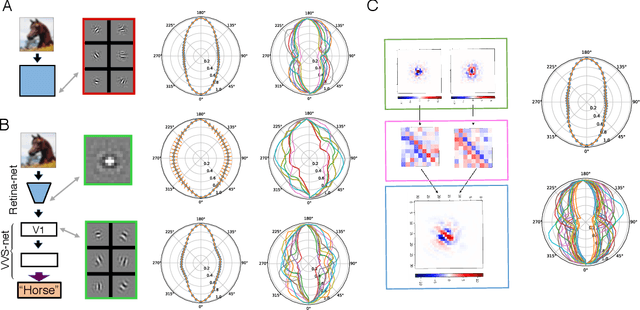
The visual system is hierarchically organized to process visual information in successive stages. Neural representations vary drastically across the first stages of visual processing: at the output of the retina, ganglion cell receptive fields (RFs) exhibit a clear antagonistic center-surround structure, whereas in the primary visual cortex, typical RFs are sharply tuned to a precise orientation. There is currently no unified theory explaining these differences in representations across layers. Here, using a deep convolutional neural network trained on image recognition as a model of the visual system, we show that such differences in representation can emerge as a direct consequence of different neural resource constraints on the retinal and cortical networks, and we find a single model from which both geometries spontaneously emerge at the appropriate stages of visual processing. The key constraint is a reduced number of neurons at the retinal output, consistent with the anatomy of the optic nerve as a stringent bottleneck. Second, we find that, for simple cortical networks, visual representations at the retinal output emerge as nonlinear and lossy feature detectors, whereas they emerge as linear and faithful encoders of the visual scene for more complex cortices. This result predicts that the retinas of small vertebrates should perform sophisticated nonlinear computations, extracting features directly relevant to behavior, whereas retinas of large animals such as primates should mostly encode the visual scene linearly and respond to a much broader range of stimuli. These predictions could reconcile the two seemingly incompatible views of the retina as either performing feature extraction or efficient coding of natural scenes, by suggesting that all vertebrates lie on a spectrum between these two objectives, depending on the degree of neural resources allocated to their visual system.