Stephane Clinchant
Composite Code Sparse Autoencoders for first stage retrieval
Apr 14, 2022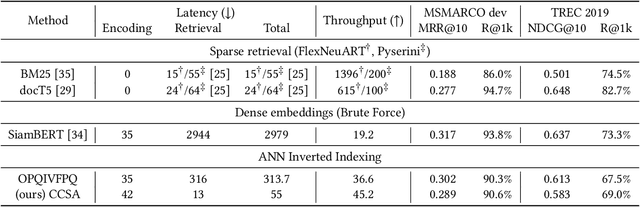
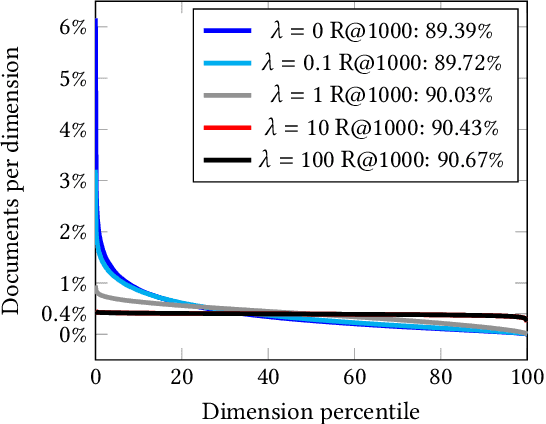
Abstract:We propose a Composite Code Sparse Autoencoder (CCSA) approach for Approximate Nearest Neighbor (ANN) search of document representations based on Siamese-BERT models. In Information Retrieval (IR), the ranking pipeline is generally decomposed in two stages: the first stage focus on retrieving a candidate set from the whole collection. The second stage re-ranks the candidate set by relying on more complex models. Recently, Siamese-BERT models have been used as first stage ranker to replace or complement the traditional bag-of-word models. However, indexing and searching a large document collection require efficient similarity search on dense vectors and this is why ANN techniques come into play. Since composite codes are naturally sparse, we first show how CCSA can learn efficient parallel inverted index thanks to an uniformity regularizer. Second, CCSA can be used as a binary quantization method and we propose to combine it with the recent graph based ANN techniques. Our experiments on MSMARCO dataset reveal that CCSA outperforms IVF with product quantization. Furthermore, CCSA binary quantization is beneficial for the index size, and memory usage for the graph-based HNSW method, while maintaining a good level of recall and MRR. Third, we compare with recent supervised quantization methods for image retrieval and find that CCSA is able to outperform them.
An Extended Framework for Marginalized Domain Adaptation
Feb 20, 2017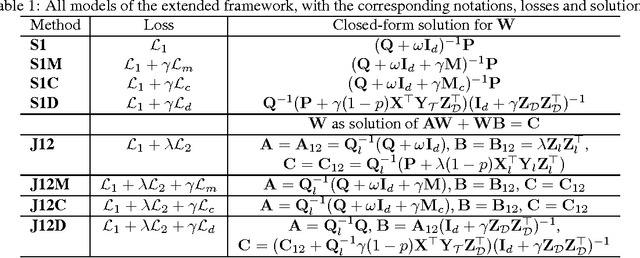
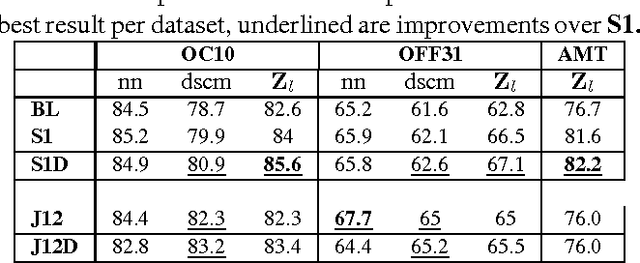
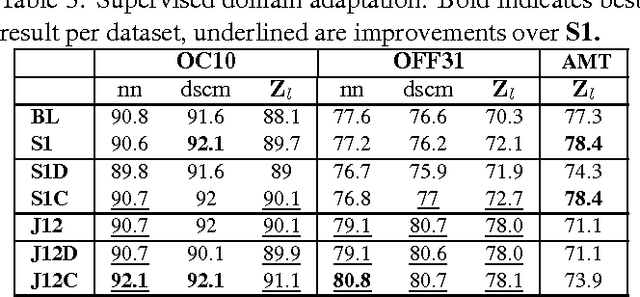
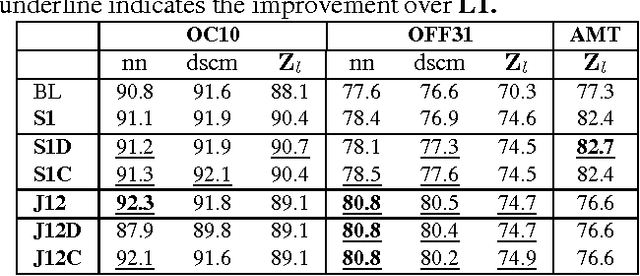
Abstract:We propose an extended framework for marginalized domain adaptation, aimed at addressing unsupervised, supervised and semi-supervised scenarios. We argue that the denoising principle should be extended to explicitly promote domain-invariant features as well as help the classification task. Therefore we propose to jointly learn the data auto-encoders and the target classifiers. First, in order to make the denoised features domain-invariant, we propose a domain regularization that may be either a domain prediction loss or a maximum mean discrepancy between the source and target data. The noise marginalization in this case is reduced to solving the linear matrix system $AX=B$ which has a closed-form solution. Second, in order to help the classification, we include a class regularization term. Adding this component reduces the learning problem to solving a Sylvester linear matrix equation $AX+BX=C$, for which an efficient iterative procedure exists as well. We did an extensive study to assess how these regularization terms improve the baseline performance in the three domain adaptation scenarios and present experimental results on two image and one text benchmark datasets, conventionally used for validating domain adaptation methods. We report our findings and comparison with state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge