Complexity Results and Practical Algorithms for Logics in Knowledge Representation

Description Logics (DLs) are used in knowledge-based systems to represent and reason about terminological knowledge of the application domain in a semantically well-defined manner. In this thesis, we establish a number of novel complexity results and give practical algorithms for expressive DLs that provide different forms of counting quantifiers. We show that, in many cases, adding local counting in the form of qualifying number restrictions to DLs does not increase the complexity of the inference problems, even if binary coding of numbers in the input is assumed. On the other hand, we show that adding different forms of global counting restrictions to a logic may increase the complexity of the inference problems dramatically. We provide exact complexity results and a practical, tableau based algorithm for the DL SHIQ, which forms the basis of the highly optimized DL system iFaCT. Finally, we describe a tableau algorithm for the clique guarded fragment (CGF), which we hope will serve as the basis for an efficient implementation of a CGF reasoner.

Reasoning with Individuals for the Description Logic SHIQ

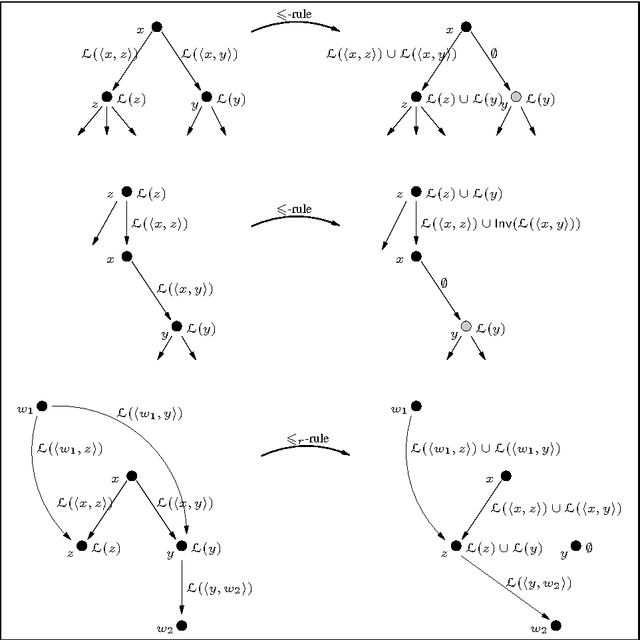
While there has been a great deal of work on the development of reasoning algorithms for expressive description logics, in most cases only Tbox reasoning is considered. In this paper we present an algorithm for combined Tbox and Abox reasoning in the SHIQ description logic. This algorithm is of particular interest as it can be used to decide the problem of (database) conjunctive query containment w.r.t. a schema. Moreover, the realisation of an efficient implementation should be relatively straightforward as it can be based on an existing highly optimised implementation of the Tbox algorithm in the FaCT system.

Practical Reasoning for Expressive Description Logics

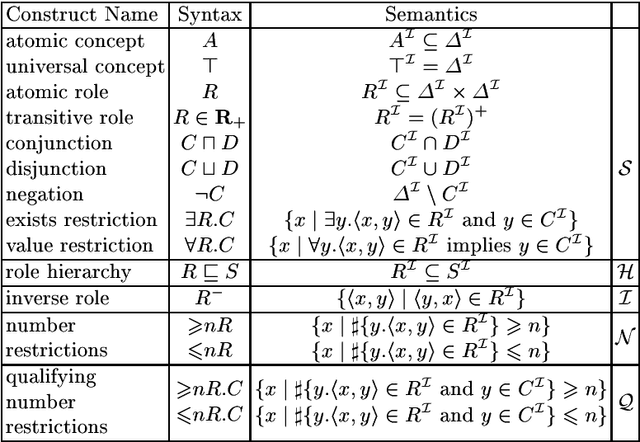
Description Logics (DLs) are a family of knowledge representation formalisms mainly characterised by constructors to build complex concepts and roles from atomic ones. Expressive role constructors are important in many applications, but can be computationally problematical. We present an algorithm that decides satisfiability of the DL ALC extended with transitive and inverse roles, role hierarchies, and qualifying number restrictions. Early experiments indicate that this algorithm is well-suited for implementation. Additionally, we show that ALC extended with just transitive and inverse roles is still in PSPACE. Finally, we investigate the limits of decidability for this family of DLs.

Practical Reasoning for Very Expressive Description Logics

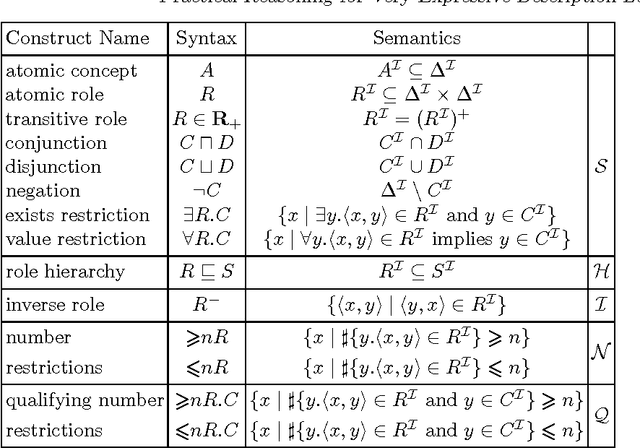
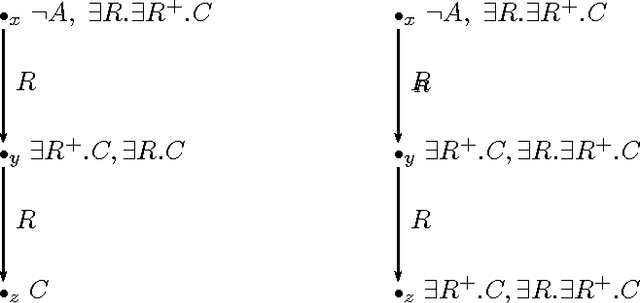
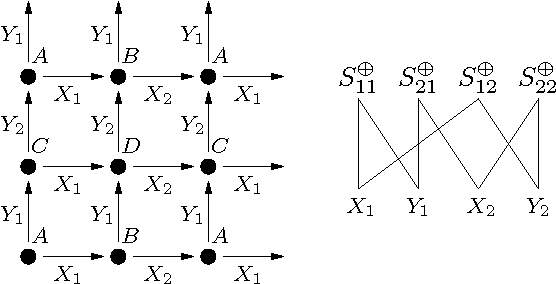
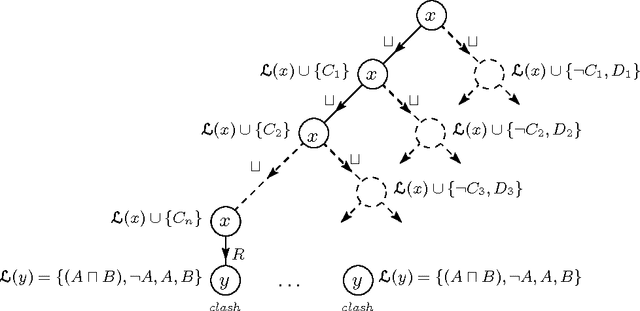
Description Logics (DLs) are a family of knowledge representation formalisms mainly characterised by constructors to build complex concepts and roles from atomic ones. Expressive role constructors are important in many applications, but can be computationally problematical. We present an algorithm that decides satisfiability of the DL ALC extended with transitive and inverse roles and functional restrictions with respect to general concept inclusion axioms and role hierarchies; early experiments indicate that this algorithm is well-suited for implementation. Additionally, we show that ALC extended with just transitive and inverse roles is still in PSPACE. We investigate the limits of decidability for this family of DLs, showing that relaxing the constraints placed on the kinds of roles used in number restrictions leads to the undecidability of all inference problems. Finally, we describe a number of optimisation techniques that are crucial in obtaining implementations of the decision procedures, which, despite the worst-case complexity of the problem, exhibit good performance with real-life problems.

Reasoning with Axioms: Theory and Pratice

When reasoning in description, modal or temporal logics it is often useful to consider axioms representing universal truths in the domain of discourse. Reasoning with respect to an arbitrary set of axioms is hard, even for relatively inexpressive logics, and it is essential to deal with such axioms in an efficient manner if implemented systems are to be effective in real applications. This is particularly relevant to Description Logics, where subsumption reasoning with respect to a terminology is a fundamental problem. Two optimisation techniques that have proved to be particularly effective in dealing with terminologies are lazy unfolding and absorption. In this paper we seek to improve our theoretical understanding of these important techniques. We define a formal framework that allows the techniques to be precisely described, establish conditions under which they can be safely applied, and prove that, provided these conditions are respected, subsumption testing algorithms will still function correctly. These results are used to show that the procedures used in the FaCT system are correct and, moreover, to show how efficiency can be significantly improved, while still retaining the guarantee of correctness, by relaxing the safety conditions for absorption.

PSPACE Reasoning for Graded Modal Logics

We present a PSPACE algorithm that decides satisfiability of the graded modal logic Gr(K_R)---a natural extension of propositional modal logic K_R by counting expressions---which plays an important role in the area of knowledge representation. The algorithm employs a tableaux approach and is the first known algorithm which meets the lower bound for the complexity of the problem. Thus, we exactly fix the complexity of the problem and refute an ExpTime-hardness conjecture. We extend the results to the logic Gr(K_(R \cap I)), which augments Gr(K_R) with inverse relations and intersection of accessibility relations. This establishes a kind of ``theoretical benchmark'' that all algorithmic approaches can be measured against.