Practical Reasoning for Very Expressive Description Logics

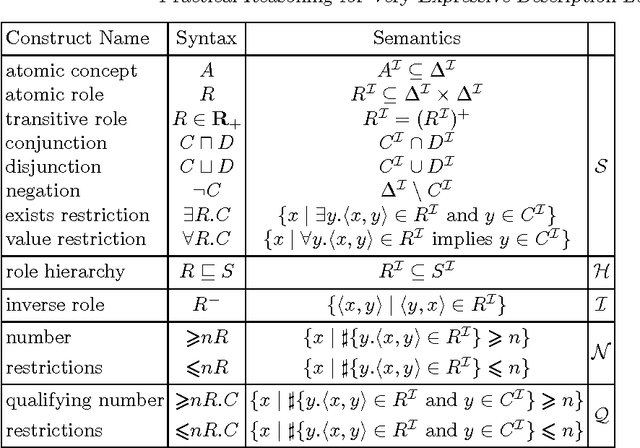
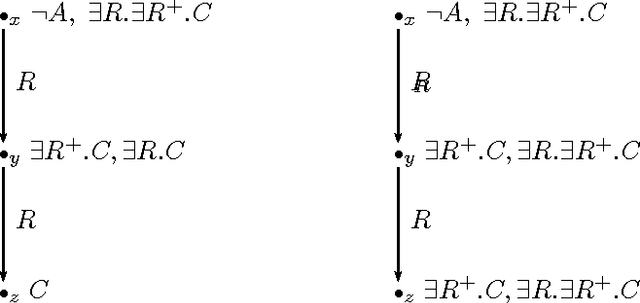
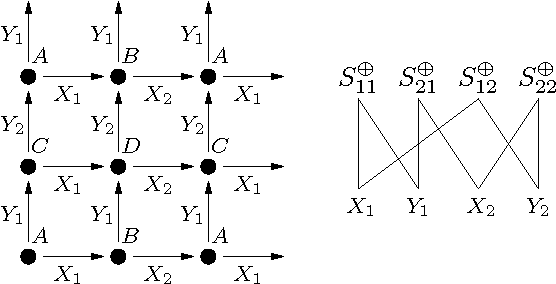
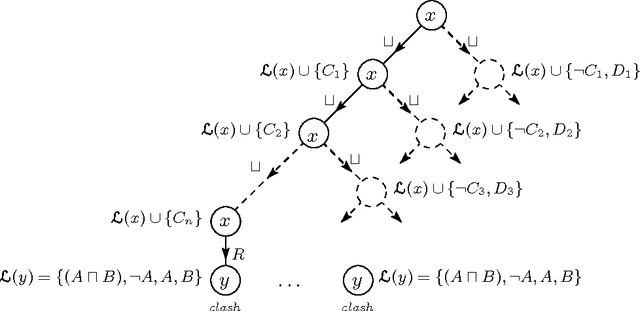
Description Logics (DLs) are a family of knowledge representation formalisms mainly characterised by constructors to build complex concepts and roles from atomic ones. Expressive role constructors are important in many applications, but can be computationally problematical. We present an algorithm that decides satisfiability of the DL ALC extended with transitive and inverse roles and functional restrictions with respect to general concept inclusion axioms and role hierarchies; early experiments indicate that this algorithm is well-suited for implementation. Additionally, we show that ALC extended with just transitive and inverse roles is still in PSPACE. We investigate the limits of decidability for this family of DLs, showing that relaxing the constraints placed on the kinds of roles used in number restrictions leads to the undecidability of all inference problems. Finally, we describe a number of optimisation techniques that are crucial in obtaining implementations of the decision procedures, which, despite the worst-case complexity of the problem, exhibit good performance with real-life problems.