Latent Space Subdivision: Stable and Controllable Time Predictions for Fluid Flow

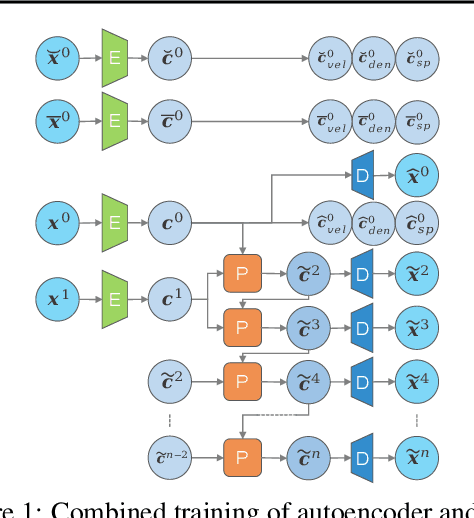
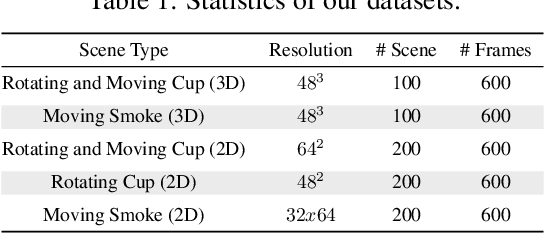
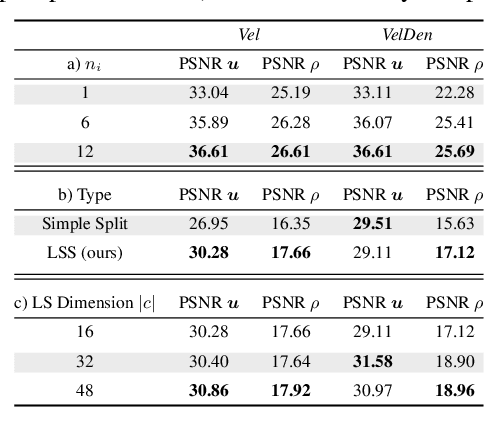
We propose an end-to-end trained neural networkarchitecture to robustly predict the complex dynamics of fluid flows with high temporal stability. We focus on single-phase smoke simulations in 2D and 3D based on the incompressible Navier-Stokes (NS) equations, which are relevant for a wide range of practical problems. To achieve stable predictions for long-term flow sequences, a convolutional neural network (CNN) is trained for spatial compression in combination with a temporal prediction network that consists of stacked Long Short-Term Memory (LSTM) layers. Our core contribution is a novel latent space subdivision (LSS) to separate the respective input quantities into individual parts of the encoded latent space domain. This allows to distinctively alter the encoded quantities without interfering with the remaining latent space values and hence maximizes external control. By selectively overwriting parts of the predicted latent space points, our proposed method is capable to robustly predict long-term sequences of complex physics problems. In addition, we highlight the benefits of a recurrent training on the latent space creation, which is performed by the spatial compression network.

Latent-space Physics: Towards Learning the Temporal Evolution of Fluid Flow

Our work explores methods for the data-driven inference of temporal evolutions of physical functions with deep learning techniques. More specifically, we target fluid flow problems, and we propose a novel LSTM-based approach to predict the changes of the pressure field over time. The central challenge in this context is the high dimensionality of Eulerian space-time data sets. Key for arriving at a feasible algorithm is a technique for dimensionality reduction based on convolutional neural networks, as well as a special architecture for temporal prediction. We demonstrate that dense 3D+time functions of physics system can be predicted with neural networks, and we arrive at a neural-network based simulation algorithm with significant practical speed-ups. We demonstrate the capabilities of our method with a series of complex liquid simulations, and with a set of single-phase buoyancy simulations. With a set of trained networks, our method is more than two orders of magnitudes faster than a traditional pressure solver. Additionally, we present and discuss a series of detailed evaluations for the different components of our algorithm.