Bayesian full waveform inversion with sequential surrogate model refinement

Bayesian formulations of inverse problems are attractive for their ability to incorporate prior knowledge and update probabilistic models as new data become available. Markov chain Monte Carlo (MCMC) methods sample posterior probability density functions (pdfs) but require accurate prior models and many likelihood evaluations. Dimensionality-reduction methods, such as principal component analysis (PCA), can help define the prior and train surrogate models that efficiently approximate costly forward solvers. However, for problems like full waveform inversion, the complex input/output relations often cannot be captured well by surrogate models trained only on prior samples, leading to biased results. Including samples from high-posterior-probability regions can improve accuracy, but these regions are hard to identify in advance. We propose an iterative method that progressively refines the surrogate model. Starting with low-frequency data, we train an initial surrogate and perform an MCMC inversion. The resulting posterior samples are then used to retrain the surrogate, allowing us to expand the frequency bandwidth in the next inversion step. Repeating this process reduces model errors and improves the surrogate's accuracy over the relevant input domain. Ultimately, we obtain a highly accurate surrogate across the full bandwidth, enabling a final MCMC inversion. Numerical results from 2D synthetic crosshole Ground Penetrating Radar (GPR) examples show that our method outperforms ray-based approaches and those relying solely on prior sampling. The overall computational cost is reduced by about two orders of magnitude compared to full finite-difference time-domain modeling.

Reliability analysis for non-deterministic limit-states using stochastic emulators

Reliability analysis is a sub-field of uncertainty quantification that assesses the probability of a system performing as intended under various uncertainties. Traditionally, this analysis relies on deterministic models, where experiments are repeatable, i.e., they produce consistent outputs for a given set of inputs. However, real-world systems often exhibit stochastic behavior, leading to non-repeatable outcomes. These so-called stochastic simulators produce different outputs each time the model is run, even with fixed inputs. This paper formally introduces reliability analysis for stochastic models and addresses it by using suitable surrogate models to lower its typically high computational cost. Specifically, we focus on the recently introduced generalized lambda models and stochastic polynomial chaos expansions. These emulators are designed to learn the inherent randomness of the simulator's response and enable efficient uncertainty quantification at a much lower cost than traditional Monte Carlo simulation. We validate our methodology through three case studies. First, using an analytical function with a closed-form solution, we demonstrate that the emulators converge to the correct solution. Second, we present results obtained from the surrogates using a toy example of a simply supported beam. Finally, we apply the emulators to perform reliability analysis on a realistic wind turbine case study, where only a dataset of simulation results is available.

A comprehensive framework for multi-fidelity surrogate modeling with noisy data: a gray-box perspective

Computer simulations (a.k.a. white-box models) are more indispensable than ever to model intricate engineering systems. However, computational models alone often fail to fully capture the complexities of reality. When physical experiments are accessible though, it is of interest to enhance the incomplete information offered by computational models. Gray-box modeling is concerned with the problem of merging information from data-driven (a.k.a. black-box) models and white-box (i.e., physics-based) models. In this paper, we propose to perform this task by using multi-fidelity surrogate models (MFSMs). A MFSM integrates information from models with varying computational fidelity into a new surrogate model. The multi-fidelity surrogate modeling framework we propose handles noise-contaminated data and is able to estimate the underlying noise-free high-fidelity function. Our methodology emphasizes on delivering precise estimates of the uncertainty in its predictions in the form of confidence and prediction intervals, by quantitatively incorporating the different types of uncertainty that affect the problem, arising from measurement noise and from lack of knowledge due to the limited experimental design budget on both the high- and low-fidelity models. Applied to gray-box modeling, our MFSM framework treats noisy experimental data as the high-fidelity and the white-box computational models as their low-fidelity counterparts. The effectiveness of our methodology is showcased through synthetic examples and a wind turbine application.

Efficient Bayesian travel-time tomography with geologically-complex priors using sensitivity-informed polynomial chaos expansion and deep generative networks

Monte Carlo Markov Chain (MCMC) methods commonly confront two fundamental challenges: the accurate characterization of the prior distribution and the efficient evaluation of the likelihood. In the context of Bayesian studies on tomography, principal component analysis (PCA) can in some cases facilitate the straightforward definition of the prior distribution, while simultaneously enabling the implementation of accurate surrogate models based on polynomial chaos expansion (PCE) to replace computationally intensive full-physics forward solvers. When faced with scenarios where PCA does not offer a direct means of easily defining the prior distribution alternative methods like deep generative models (e.g., variational autoencoders (VAEs)), can be employed as viable options. However, accurately producing a surrogate capable of capturing the intricate non-linear relationship between the latent parameters of a VAE and the outputs of forward modeling presents a notable challenge. Indeed, while PCE models provide high accuracy when the input-output relationship can be effectively approximated by relatively low-degree multivariate polynomials, this condition is typically unmet when utilizing latent variables derived from deep generative models. In this contribution, we present a strategy that combines the excellent reconstruction performances of VAE in terms of prio representation with the accuracy of PCA-PCE surrogate modeling in the context of Bayesian ground penetrating radar (GPR) travel-time tomography. Within the MCMC process, the parametrization of the VAE is leveraged for prior exploration and sample proposal. Concurrently, modeling is conducted using PCE, which operates on either globally or locally defined principal components of the VAE samples under examination.

Emulating the dynamics of complex systems using autoregressive models on manifolds (mNARX)

In this study, we propose a novel surrogate modelling approach to efficiently and accurately approximate the response of complex dynamical systems driven by time-varying exogenous excitations over extended time periods. Our approach, that we name \emph{manifold nonlinear autoregressive modelling with exogenous input} (mNARX), involves constructing a problem-specific exogenous input manifold that is optimal for constructing autoregressive surrogates. The manifold, which forms the core of mNARX, is constructed incrementally by incorporating the physics of the system, as well as prior expert- and domain- knowledge. Because mNARX decomposes the full problem into a series of smaller sub-problems, each with a lower complexity than the original, it scales well with the complexity of the problem, both in terms of training and evaluation costs of the final surrogate. Furthermore, mNARX synergizes well with traditional dimensionality reduction techniques, making it highly suitable for modelling dynamical systems with high-dimensional exogenous inputs, a class of problems that is typically challenging to solve.Since domain knowledge is particularly abundant in physical systems, such as those found in engineering applications, mNARX is well suited for these applications. We demonstrate that mNARX outperforms traditional autoregressive surrogates in predicting the response of a classical coupled spring-mass system excited by a one-dimensional random excitation. Additionally, we show that mNARX is well suited for emulating very high-dimensional time- and state-dependent systems, even when affected by active controllers, by surrogating the dynamics of a realistic aero-servo-elastic onshore wind turbine simulator. In general, our results demonstrate that mNARX offers promising prospects for modelling complex dynamical systems, in terms of accuracy and efficiency.

Sparse Polynomial Chaos Expansions: Solvers, Basis Adaptivity and Meta-selection

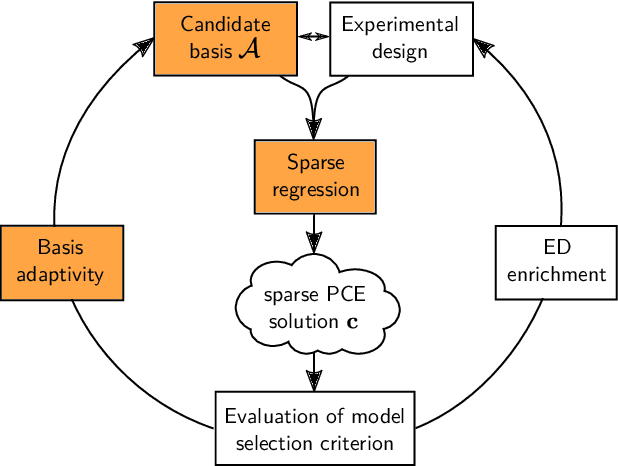
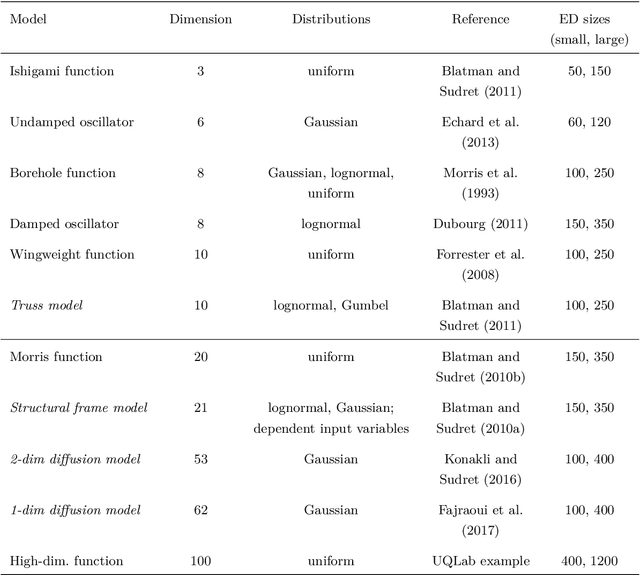
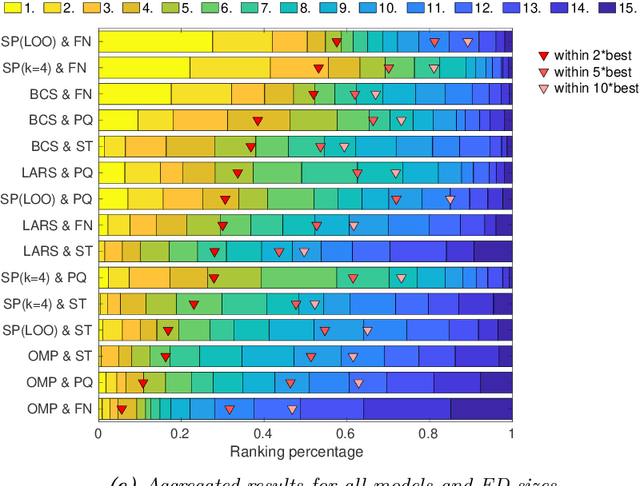
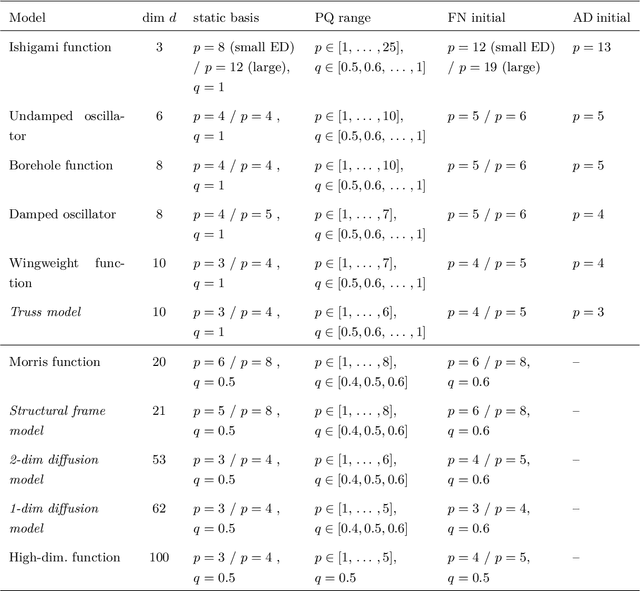
Sparse polynomial chaos expansions (PCEs) are an efficient and widely used surrogate modeling method in uncertainty quantification. Among the many contributions aiming at computing an accurate sparse PCE while using as few model evaluations as possible, basis adaptivity is a particularly interesting approach. It consists in starting from an expansion with a small number of polynomial terms, and then parsimoniously adding and removing basis functions in an iterative fashion. We describe several state-of-the-art approaches from the recent literature and extensively benchmark them on a large set of computational models representative of a wide range of engineering problems. We investigate the synergies between sparse regression solvers and basis adaptivity schemes, and provide recommendations on which of them are most promising for specific classes of problems. Furthermore, we explore the performance of a novel cross-validation-based solver and basis adaptivity selection scheme, which consistently provides close-to-optimal results.