Robust Multilinear Principal Component Analysis

Multilinear Principal Component Analysis (MPCA) is an important tool for analyzing tensor data. It performs dimension reduction similar to PCA for multivariate data. However, standard MPCA is sensitive to outliers. It is highly influenced by observations deviating from the bulk of the data, called casewise outliers, as well as by individual outlying cells in the tensors, so-called cellwise outliers. This latter type of outlier is highly likely to occur in tensor data, as tensors typically consist of many cells. This paper introduces a novel robust MPCA method that can handle both types of outliers simultaneously, and can cope with missing values as well. This method uses a single loss function to reduce the influence of both casewise and cellwise outliers. The solution that minimizes this loss function is computed using an iteratively reweighted least squares algorithm with a robust initialization. Graphical diagnostic tools are also proposed to identify the different types of outliers that have been found by the new robust MPCA method. The performance of the method and associated graphical displays is assessed through simulations and illustrated on two real datasets.

Split Modeling for High-Dimensional Logistic Regression

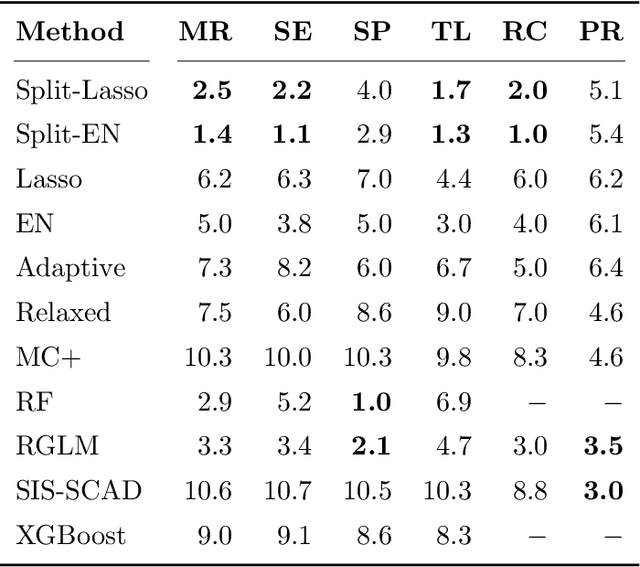
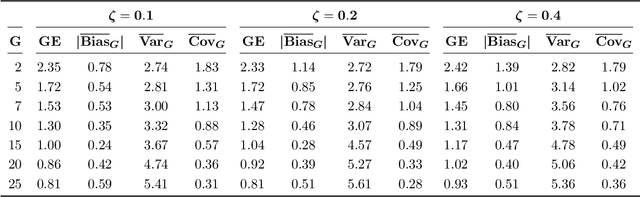
A novel method is proposed to learn an ensemble of logistic classification models in the context of high-dimensional binary classification. The models in the ensemble are built simultaneously by optimizing a multi-convex objective function. To enforce diversity between the models the objective function penalizes overlap between the models in the ensemble. We study the bias and variance of the individual models as well as their correlation and discuss how our method learns the ensemble by exploiting the accuracy-diversity trade-off for ensemble models. In contrast to other ensembling approaches, the resulting ensemble model is fully interpretable as a logistic regression model and at the same time yields excellent prediction accuracy as demonstrated in an extensive simulation study and gene expression data applications. An open-source compiled software library implementing the proposed method is briefly discussed.

On the stability of bootstrap estimators

It is shown that bootstrap approximations of an estimator which is based on a continuous operator from the set of Borel probability measures defined on a compact metric space into a complete separable metric space is stable in the sense of qualitative robustness. Support vector machines based on shifted loss functions are treated as special cases.